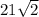Найдите высоту правильной четырехугольной пирамиды, если сторона основания равна 6 см и боковое ребро 30 см. ответ должен получиться: 21 корень из 2
Другие вопросы по теме Алгебра
Популярные вопросы
- Что роднит лужина и раскольникова? четко и ясно,можно как то сравнить,можно...
2 - Напишите как пишется и проверочное слово. хорош** самочу*ствие,пол*галось,свеж*стью...
3 - Сравнительная характеристика героев рассказа тихое утро яшки и володи...
2 - Вшар радиусом 14 см вписана правильная треугольная призма с диагональю боковой...
3 - Черепаха повзла1,5год зі швидкістю15,3м/год і 3,5год-зі швидкістю 12,4м/год,...
2 - Процентная концентрация соли 14% сколько грамм соли содержится в 2 кг этого...
3 - (720-t×6): 9=60 720-t×6= 720-t×6= 720-t= 720-t= t= t=...
2 - Установите соответствие между двумя веществами и реактивом с которого можно...
1 - Назови страны евразии, расположенные на побережье....
2 - Вклассе 30 учащихся в игре участвуют две пятых всех учащихся класса сколько...
1
Диагональ основы равна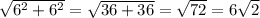
Половина диагонали равна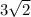
И по теореме Пифагора находим высоту:
h=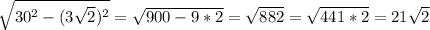
Высота пиравиды