Найдите все значения при каждом из которых наибольшее значение выражения
(a-x)(x+4) больше 4

Это выражение представляет собой квадратный трехчлен. Раскрыв скобки, получим:

-x² - 4x + 4a + ax

Приведем его к виду αx² + βx + c:

-x² - x(4 - a) + 4a

Т.к α = -1, то ветви параболы всегда будут направлены вниз, а её вершина будет точкой максимума. Нам нужно, чтобы значение выражения при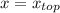 было больше 4. 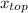= - β/2α = (a - 4) / 2. Теперь это нужно подставить в исходное уравнение и решить неравенство:

a ∈ (-∞; 0)∪(8; +∞)

ответ: (-∞; 0)∪(8; +∞)