1. Алгебра
  2. Найдите все значения параметра

Найдите все значения параметра а при каждом из которых уравнене x²+3x-9a+18=0 и x²+6x-13a+25=0 имеют хотя бы один общий корень. решите с подробным решением.

Alisascol Alisascol    2   31.07.2019 23:10    3

Ответы
умная196 умная196  03.10.2020 19:09
Для решения этой задачи достаточно просто решить систему уравнений:
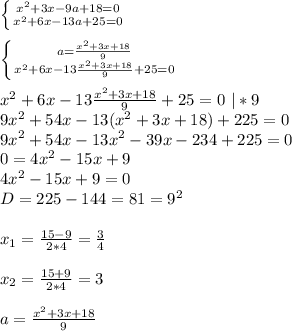
\left \{ {{x^2+3x-9a+18=0 } \atop {x^2+6x-13a+25=0 }} \right. \\ \\ \left \{ {{a= \frac{x^2+3x+18}{9} } \atop {x^2+6x-13\frac{x^2+3x+18}{9}+25=0}} \right. \\ \\ x^2+6x-13\frac{x^2+3x+18}{9}+25=0\ |*9 \\ 9 x^{2} +54x-13(x^2+3x+18)+225=0 \\ 9 x^{2} +54x-13 x^{2} -39x-234+225=0 \\ 0=4 x^{2} -15x+9 \\ 4x^{2} -15x+9=0 \\ D= 225-144=81=9^2 \\ \\ x_1= \frac{15-9}{2*4}= \frac{3}{4} \\ \\ x_2= \frac{15+9}{2*4} =3 \\ \\ a= \frac{x^2+3x+18}{9} \\
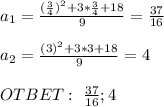
a_1= \frac{(\frac{3}{4})^2+3*\frac{3}{4}+18}{9}= \frac{37}{16} \\ \\ a_2= \frac{(3)^2+3*3+18}{9}=4 \\ \\ OTBET: \ \frac{37}{16}; 4
ПОКАЗАТЬ ОТВЕТЫ
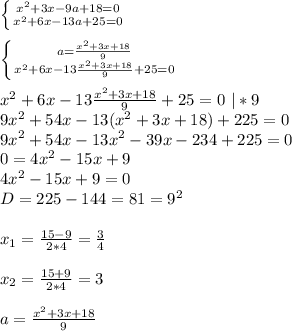
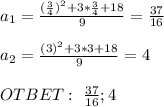
Другие вопросы по теме Алгебра
mari200423 mari200423  23.06.2019 17:10
Найдите производную функции y=x^2-7x и y=-3x^2-13x...
kolya1123 kolya1123  23.06.2019 17:10
3(-2x+1)-2(x+13)=7x-4(1-x) решите уравнение...
ДашаЛис56 ДашаЛис56  23.06.2019 17:10
Найти знаменатель прогрессии если а3=2 а6=1/4...
sawbee sawbee  23.06.2019 17:10
Решите квадратное уравнение 5 x^{2} +14x-3=0...
Karta2346574 Karta2346574  23.06.2019 17:10
Раскройте скобки и найдите значение выражения : а) 3,,3+3,7) б) -0,56+(3,8-2,44)...
NazarKlakovych28 NazarKlakovych28  23.06.2019 17:10
Высота конуса равна 21, а длина образующей равна 29. найдите диаметр основания конуса...
Dasha8999 Dasha8999  23.06.2019 17:10
Какое число будет следущем ряду 774; 823; 887; 968;...
raivon2005new raivon2005new  23.06.2019 17:10
Не выполняя вычислений, сравните значения выражений 2712+4672 и (271+467)2 выберите правильный ответ: 2712+4672=(271+467)2 2712+4672 (271+467)2 2712+4672 (271+467)2...
burkhanovshukh burkhanovshukh  23.06.2019 17:10
Прогрессия вычислите сумму 2 первых членов,если b4= -24,q=-2...
Groza11 Groza11  26.01.2021 21:26
Найди значение выражения sin1410°+cos3180°+tg1035°/−3...

Популярные вопросы