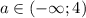Найдите все значения параметра а, при каждом из которых ур-е имеет 1 решение: x^3-x+2=-x^2+ax-1
Другие вопросы по теме Алгебра
Популярные вопросы
- Напишите интерьер дома из сказок( минимум 3)...
1 - Задайте к каждому предложению вопрос на языке! 1. my sister gets up at...
3 - Все термины, ниже, за исключением одного, связаны с понятием «социальная...
2 - Если каждая фигура означает определенное число,то какое число обозначено...
3 - Сизиф должен затащить камень на вершину горы. за день он поднимает камень...
1 - Найдите силу тяжости медного куба со стороной его = 2 см плотность медного...
2 - Что такое автобиография ? объясните происхождение этого словва.из каких...
3 - Рассчитайте какая масса осадка образуется при сливании 15г 5% раствора...
1 - А) заполни пропуски в таблице: v l d ccix mdlx 5 10 100 1000 72 б) какие...
1 - Почему торговля индульгенциями вызывала возмущение истинно верующих людей?...
1
Так как x = 0 не является корнем уравнения, поделим обе части на x.
Обозначим правую часть как f(x). Найдём производную этой функции:
Заметим, что при x = 1 числитель равен нулю. Разложим его на множители: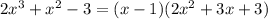 . Второй множитель разложить нельзя, так как, приравняв его к нулю, мы не сможем найти корни, ибо D < 0. Найдём знаки производной (см. фото 1). Зная это, можем прикинуть график функции (см. фото 2). Точка локального минимума - x = 1. f(1) = 4.
. Второй множитель разложить нельзя, так как, приравняв его к нулю, мы не сможем найти корни, ибо D < 0. Найдём знаки производной (см. фото 1). Зная это, можем прикинуть график функции (см. фото 2). Точка локального минимума - x = 1. f(1) = 4.
a = k (k - какое-то число) - прямая, параллельная оси Ox. По графику видно, что при a < 4 имеется ровно одно пересечение, то есть один корень.
ответ: