Найдите все значения параметра a, при каждом из которых система уравнений имеет всего 2 решения 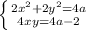
Другие вопросы по теме Алгебра
Популярные вопросы
- Ат тұмсығын тіреген жер, көбе, бадана, кіреуке деген ескірген сөздердің...
2 - у человека цвет глаз и характер волос наследуются Независимо (несцепленные)....
1 - Если бы Маша Мирнова выбрала Швабрина, то события разворачивались вот так......
1 - Скласти реченяслов із однією пару слов :загадковий,чемний,старий....
1 - X² + 8x - 33 = 0 решите через дискриминант...
1 - Задайте аналитическим числовую последовательность 1 ; -1 ; 1 ; -1...
1 - На рисунке изображена рамка с током, которая поворачивается в магнитном...
2 - Потяг довжиною 400 м проїжджає через міст за 1 хвилину. Яка довжина мосту...
3 - Сторона рівностороннього трикутника дорівнює 10√3 м....
1 - Выполнить морфологический разбор выделенных существительных 1. Стая ПТИЦ...
3
подставим 4а во второе уравнение системы. получим 4ху=2х²+2у²-2, упростим
-2ху+х²+у²=1; (х-у)²-1=0; (х-у-1)*(х-у+1)=0; 1)х=у+1 или 2)х=у-1 получили две прямые.
Если х=у+1,то 4у*(у+1)+2=а; 4у²+4у+2=а; (2у+1)²=а-1; Если а=1 ,то получим один корень, если а>1, то два корня. Если а<1, то корней нет.
Если рассмотреть первое уравнение, то при каждом a ≠ 0 — уравнение окружности c центром (0, 0) и радиусом а√2, тогда система при а=0 имеет единственное решение и поэтому не удовлетворяет условию задачи. При а≤0 уравнение не имеет смысла.
используем теперь результат выше и уточним ответ на задачу.
Если х=у+1, то у²+у²+2у+1=2а,у²+у+1/2=а; (у+1/2)²=а-1/4, при а=1/4 уравнение имеет одно решение, а при а >1/4 два различных решения.
Если х=у-1, то у²+у²-2у+1=2а,у²-у+1/2=а; (у-1/2)²=а-1/4, при а=1/4 уравнение имеет одно решение, а при а >1/4 два различных решения.