Найдите все значения х, при каждом из которых касательная к графику функции у=cos7x+7cosx в точках с абсциссой х параллельна касательной к этому же графику в точке с абсциссой пи/6
Другие вопросы по теме Алгебра
Популярные вопросы
- Хозяйка собрала 38946 килограмм слив черешен и вишен половину этого...
3 - Как изменилось мое отношение к употреблению наркотиков...
1 - Соответствия: 1. put yourself 2. don t take 3. take my 4. take it...
3 - Какое средство выразительности использованно в этом отрывке: прорвался...
2 - Встихотворении найти слова, где звуков больше, чем букв : мы собрали...
3 - При спиртовой брожении глюкозы массой 90 г выделяется оксид углерода...
1 - Визначте обьем вогулекислого газу за нормальними умовами що утворюються...
1 - Вычислите: sin^4a + cos^4a, если sina+cosa = 1/√2...
1 - Характеристика татьяны лариной. евгений онегин на одиночество...
2 - 1)zn(oh)2 + hcl = zncl2 + h2o 2)fe(no3)2+koh=fe(oh)2+kno3 3) k2co3+hci=kce+h2co3...
2
Геометрический смысл производной. Производная в точке x₀ равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке, то есть:
Предварительно вычисляем производную функции первого порядка.
Производная функции в точке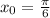
То есть, угловой коэффициент равен 0. Тогда для нахождения значения х, при каждом из которых касательная к данной функции в точках с абсциссой х параллельна касательной в точке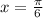 , нужно решить следующее уравнение:
, нужно решить следующее уравнение:
Произведение равно нулю, если хотя бы один из множителей равен 0.