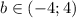Найдите все значения b ,при которых уравнение:
9^x+(b^2+6)3^x-b^2+16=0 не имеет корней
Другие вопросы по теме Алгебра
Популярные вопросы
- Органы чувств и замкнутая кровеносная система впервые появляются у кого...
3 - Перевидите предложения на яз используя past perfect : 1 что ты будешь готовиь...
1 - Дебют советской дипломатии на международной конференции в генуе произошел...
1 - Можно ли в тексте обойтись без прилагательных?...
1 - Укажите верное равенство: а-4030=4 кг 3 г. б-4030=40 кг 30 г. в-4030=4...
1 - Найди частное и остаток.выполнить проверку. 67÷9 , 28÷ 30 , 673÷4 , 489÷...
2 - Вычислить sin 69° cos21° cos 69° sin 21°...
1 - Как распростроняется электромагнитная волна в вакуме...
2 - Запиши основные сведения о своём крае...
2 - Билет на автобус стоит 30 рублей опредилите на сколько поездок хватит 100рублей...
3
Выполним замену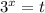 причем
причем 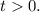 Получаем
Получаем
Дискриминант квадратного уравнения:
Если D < 0, то квадратное уравнение корней не имеет. , т.е.
Это неравенство эквивалентно двойному неравенству
При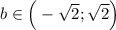 данное уравнение корней не будет иметь.
данное уравнение корней не будет иметь.
Теперь рассмотрим случай когда квадратное уравнение относительно t имеет корни, т.е.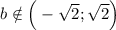 , то нам нужны отрицательные корни, поскольку при замене
, то нам нужны отрицательные корни, поскольку при замене 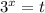 это уравнение не будет иметь корень. По теореме Виета имеем:
это уравнение не будет иметь корень. По теореме Виета имеем:
С учетом существования корней имеем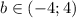
ответ: при