Найдите все значения a, такие, что уравнение |2x+1|=x+a имеет единственное решение.

(см. объяснение)

Объяснение:

Первый :

Рассмотрим функцию .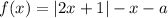

Тогда уравнение примет вид .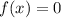

Заметим, что решающую роль на поведение функции (ее возрастание или убывание) всегда оказывает знак при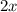 . Тогда функция убывает на промежутке , а возрастает на 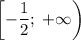. Значит единственное решение достигается тогда и только тогда, когда .

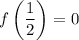Получили уравнение:

Итого при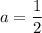 исходное уравнение имеет единственное решение.

Второй :

Построим график этого уравнения в координатах :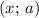

(см. прикрепленный файл)

Тогда ответом будет .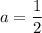

Третий :

Знаем, что при :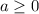

Тогда единственное решение возможно, только если .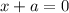

Получили уравнение:

Так как .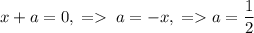

Задание выполнено!