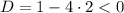Найдите все рациональные корни многочлена 2x^4+5x^3+6x^2+5x=2
Другие вопросы по теме Алгебра
Популярные вопросы
- Пирамида пересечена плоскостью, параллельной основанию. Площадь основания...
1 - Складіть програму, яка перевіряє, чи ділиться введене користувачем число на...
2 - На какие группы делится производство...
3 - Докажите неравенство: (x-5)(x+2) (x+1)(x-4)...
3 - Найдите наименьшее значение y=1/cos^2x+ctg^2+1...
1 - Приземление осуществляется боком к планке. На какую ногу? 2. Для обучения...
3 - Какие общие признаки, характерные как для естественных, так и для искусственных...
3 - ребят,очень нужно. Как можно быстрее...
3 - решить задачи по статистике!3 и 4 задачи...
3 - ищу друзей добавляйтесь (желательно с дс))...
1
Переносим все в левую часть и разложим одночлены в сумму нескольких
Произведение равно нулю в том случае, когда хотя один из множителей обращается к нулю
Это уравнение решений не имеет, так как дискриминант квадратного уравнения