Найдите вместе с дано напишите буду вам очень благодарен ой по геометрии
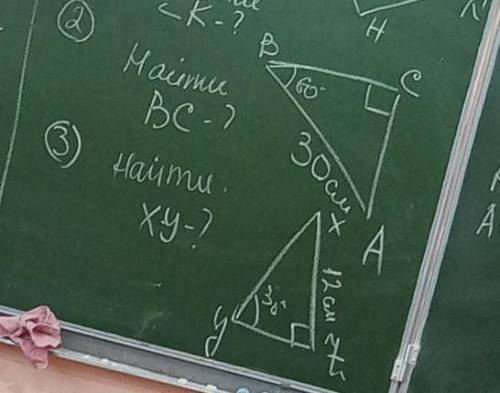
Другие вопросы по теме Алгебра
Популярные вопросы
- Задание 3. ( ) Постройте график прямой пропорциональности, заданной...
3 - .У повітрі тіло розтягнуло пружину динамометра із силою 25,1 Н,...
2 - Провідміняйте числівник сорок дві третіх...
1 - Завдання з Зарубіжної літератури Дайте відповідь на питання: «Чия...
3 - Как добрый поступок Яши повлиял на окружающих людей...
2 - У соціально-психологічних теоріях головним показником нації є...
3 - Три менеджери роблять заявки на продукцію. Нехай С=1,3 – подія,...
3 - Почему Сенека не бежал, когда Нерон приказал покончить жизнь....
1 - При зменшенні об єму газу в 2 рази його тиск збільшився на 40%....
3 - ❗️‼️ 1. Прочитайте слова: мёд, олень, синий. Сколько всего в этих...
3
2)ВС=15см;3)XY=24см.
Объяснение:
2) треугольник АВС прямоугольный, угол СВА равен 60 следовательно угол САВ равен 30. По теореме, в прямоугольном треугольнике катет лежащий против угла в 30 градусов в два раза меньше гипотенузы, т.е. в нашем случае ВС=15см.
3)Как и в первой(номер 2) задаче, здесь используется теорема о том, что в прямоугольном треугольнике катет лежащий против угла в 30 градусов вдвое меньше гипотенузы, т.е. гипотенуза вдвое больше катета и равна в нашем случае 24см.
Объяснение:
2. Дано:
АВС - прямоугольный треугольник, ∠С = 90°
АВ = 30 см
∠В = 60°
ВС - ?
∠А = 180° - 90° - 60° = 30° (сумма углов в треугольнике равна 180°)
Напротив угла 30° лежит катет, который равен половине гипотенузы:
ВС = 0,5 * АВ = 0,5 * 30 = 15 (см)
ответ: 15 см
3. Дано:
XYZ - прямоугольный треугольник, ∠Z = 90°
XZ = 12 см
∠Y = 30°
XY - ?
Напротив угла 30° лежит катет, который равен половине гипотенузы:
XY = 2 * XZ = 2 * 12 = 24 (см)
ответ: 24 см