Найдите точку минимума функции
!
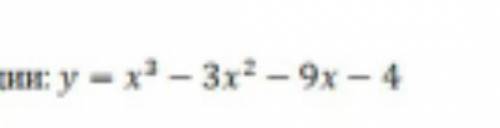
Другие вопросы по теме Алгебра
Популярные вопросы
- Сделайте алгоритм как на образце 20б 20б как можно скорее...
3 - Складіть схему Агро промисловий комплекс України...
3 - Діяльність товариства галицьких греко католицьких священиків і...
3 - Выберите выражения, которые имеют смысл: а) ⁴√(-4)⁸ б) ¹³√(-4)⁷...
3 - Стисло схарактерезуйте байки крилова?...
2 - Наведіть приклади зв язків між сільськогосподарським господарством...
1 - Электролиз водного раствора сульфата натрия с никелевыми электродами...
1 - Excel , ответы на эти вопросы Что значит решить уравнение f(x)=o?...
3 - Укажи нераспространенное предложение: Падают и кружатся листья....
1 - Можно сказать: молекула поваренной соли ?атом спирта ?атом меди...
1
ответ: xmin = 3. ymin=-31.
Объяснение:
Найдите точку минимума функции y=x³-3x²-9x-4.
Решение.
y'(x)=(x³-3x²-9x-4)'=3(x²-2x-3);
y'(x)=0; 3(x²-2x-3)=0;
x²-2x-3=0;
По т. Виета
x1+x2=2; x1*x2=-3;
x1=-1; x2=3;
Разложим на множители
3(x²-2x-3)=3(x+1)(x-3).
В точке x=3 производная меняет свой знак с "-" на "+". Следовательно эта точка является единственной точкой минимума.
f(3)=3³-3*3²-9*3-4=27-27-27-4= -31.
ответ: x min = 3. ymin= -31.