1. Алгебра
  2. Найдите точку максимума функции

Найдите точку максимума функции y=sqrt(4−4x−x2)

IrishkaLis IrishkaLis    3   11.06.2019 21:40    1

Ответы
АлександрЧерепов АлександрЧерепов  02.10.2020 00:21

y=\sqrt{4-4x-x^2}

Под знаком корня стоит квадратичная функция f (x) = 4 - 4x - x²

Графиком этой функции является парабола с ветками, направленными вниз. Максимальное значение эта функция достигает в точке вершины параболы, координаты которой вычисляются по формулам

x_0=-\dfrac{b}{2a}=-\dfrac{-4}{2\cdot (-1)}=-2\\\\f(x_0)=4 - 4\cdot (-2)-(-2)^2=4+8-4=8

Так как 8 > 0, значит, точка x₀ принадлежит области определения функции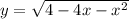 y=\sqrt{4-4x-x^2} , которая достигает своего максимального значения в точке x₀ = -2

\boldsymbol{y(-2)=\sqrt{8}=2\sqrt{2}}

Точка максимума функции x = -2

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
olgabelova51487 olgabelova51487  27.04.2021 19:22
Найдите координаты точки пересечения графиков линейных функций у = 7х – 2 и у = 3х + 10. 2) Найдите значение аргумента, при котором линейная функция у = – 2х + 7...
Danik119200 Danik119200  27.04.2021 19:22
При каких значениях а система уравнений 3x+ay=15 6x-8y=30 имеет много решений x-3y=4 ax-18y=24 имеет одно решение...
Сирунс Сирунс  27.04.2021 19:22
Докажите тождество: б) 1 + cos a - sin a / 1 - cos a - sin = -ctg a/2​...
Igor2000Petrov Igor2000Petrov  27.04.2021 19:21
Найдите точку пересечения с осьюx y) kx+b​...
ppn01012014 ppn01012014  27.04.2021 19:20
Решите уравнение (( НЕ ИГНОРЬТЕ :(​...
SadPlayer007 SadPlayer007  05.09.2019 11:40
Найдите производную функцию f (x)=1+cosx/sinx...
валерія346 валерія346  05.09.2019 11:40
Выражения а) √18(√6-√2)-3√12= б)(√15+√5)√15-5/3(дробью) * √27=...
shalaeva03 shalaeva03  05.09.2019 11:40
45 в 10 ст дробью на 5 в 8 степени * на 3 19ст...
Bereke2006 Bereke2006  05.09.2019 11:40
Один килограмм сыра стоит 278 рублей. покупатель приобрел 400 г сыра и батон за 32 рубля. сколько сдачи (в рублях) он должен получить с 500 рублей...
СофияKomarova СофияKomarova  05.09.2019 11:30
Решить )) хоть одну 1. для лагеря купили 10 мячей и 5 ракеток. один мяч стоит a рублей, а одна ракетка – b рублей. написать выражение стоимости всей покупки. 2....

Популярные вопросы