Найдите точку максимума функции: , с подробнейшим решением.

Ответы

ekaterina7201 24.05.2020 15:30

Находим производную

y'=-2/3*3/2sqrt(x)+3=-sqrt(x)+3

находим критическую точку приравняв к нулю произодную

y'=0

x=9

проверяем что точка является точкой максимума, для чего находим вторую производную

y''=-1/2sqrt(x)<0

она меньше нуля поэтому в точке имеется максимум.

y(9)-max=-2/3*27+27+1=10

ПОКАЗАТЬ ОТВЕТЫ

6473089 24.05.2020 15:30

Для исследования функции сначала нужно взять производную. Чтобы проще было взять воспользуемся формулой сложения степеней: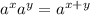 $a^xa^y=a^{x+y}$

Получим что: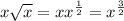 $x\sqrt{x}=xx^{\frac{1}{2}}=x^{\frac{3}{2}}$

Теперь перепишем функцию:

$y=-\frac{2}{3}x^{\frac{3}{2}}+3x+1$

И берем производную:

$y'=-\frac{2}{3}\frac{3}{2}x^{\frac{1}{2}}+3=3-\sqrt{x}$

Дальше найдем точку где производная обращается в 0.

Для этого решаем уравнение: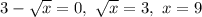 $3-\sqrt{x}=0, \ \sqrt{x}=3, \ x=9$

Это будет точка экстремума. Но точка экстремума может быть как минимумом так и максимумом. Надо показать что это максимум. Как это делается. Есть 2 метода.
1 метод:

Рассмотрим как ведет себя производная при x<9 и при x>9. Очевидно, что при x>9 производная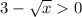 $3-\sqrt{x}0$ . Значит функция растет. При x>9, наоборот $3-\sqrt{x}<0[/tex]. Значит функция убывает. Если до точки х=9 функция растет, а после нее убывает, то получается что это максимум функции</p
<p </p
<p2 метод:</p
<pВозьмем вторую производную от исходной функции получим [tex]y''=-\frac{1}{2\sqrt{x}}$ . Для любых положительных х, вторая производная будет меньше нуля, т.е y''<0. Это необходимое и достаточное условие, чтобы функция была выпуклой вверх. Т.к. функция выпулкая вверх, то точка экстремума будет точкой максимума. ч.т.д