Найдите точки экстремума функции y=x+√3-x
Другие вопросы по теме Алгебра
Популярные вопросы
- Решить линейное неравенство|x-3| =1,8...
1 - У840 кг.готовой ягодной карамели одна седьмая всей массы становят ягоды,одна четвертая...
1 - Антоним к слову робкий . что-то вроде открытый , но по-другому...
1 - Основные экологические проблемы казахстана и государств центральной азии? пути решения...
1 - There earrings/good quality gold/are excellent value(plus)...
3 - Сочинение на тему мой папа служил в армии...
1 - Какое слово может быть только одной частью речи? выберите вариант ответа: жгут жив...
1 - Как решить уравнение чтобы получилось 0? 0=-3х-4...
1 - Найдите значение чисел 10110110 (два внизу) 21021(три внизу) 566(семь внизу) 67(восемь...
2 - Составте из словосочитаний предложения: согласно, распоряжению, приказу, решению,...
3
Область определения :
3 - x ≥ 0 ⇒ x ≤ 3
y`=(x)`+(√3-x)`
y` = 1 +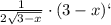
y`=1 -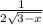
y`=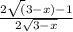
y`=0
2√(3-x)-1=0
√(3-x) =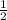
3-x =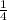
x =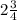
у` > 0 на (-∞;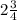 );
);
y` < 0 на (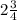 ; + ∞)
; + ∞)
х=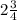 - точка максимума, производная меняет знак с + на -
- точка максимума, производная меняет знак с + на -
О т в е т. х=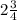 - точка максимума
- точка максимума