1. Алгебра
  2. Найдите сумму всех трёхзначных

Найдите сумму всех трёхзначных чисел, кратных 7

айка2108 айка2108    2   19.08.2019 06:20    0

Ответы
kiryakuantseva kiryakuantseva  05.10.2020 04:16

105, 112, ... , 994 - последовательность трехзначных чисел, кратных 7. Эта последовательность является арифметической прогрессией с первым членом прогрессии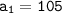 \tt a_1=105 и разность прогрессии: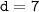 \tt d=7

По формуле n-го члена арифметической прогрессии: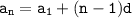 \tt a_n=a_1+(n-1)d найдем количество трехзначных чисел, кратных 7.

\tt 994=105+7(n-1)~~|:7\\ ~~~142=15+n-1\\ ~~~~~~~~~n=128

То есть, всего таких трехзначных чисел: 128. Осталось теперь вычислить сумму первых 128 членов арифметической прогрессии:

\tt S_{128}=\dfrac{2a_1+127d}{2}\cdot128=64\cdot(2\cdot105+127\cdot7)=64\cdot1099=70336



ответ: 70336.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
anaraermus anaraermus  12.05.2021 15:25
Упростите и вычислите значения при a=0,55 2a/a-5- 5/a+5 + 2a^3/25-a^2​...
mialoma mialoma  12.05.2021 15:25
позяуфста выполните действия 1. 10x-9/17x+3x-25/17x 2. 5a^2+b^2/ab-3a-2b/b Если не понятно смотри картинку...
Lerka2004love Lerka2004love  12.05.2021 15:24
11.Знайдіть тангенс кута нахилу до осі абсцис дотичної до графіка функції f(x) = x 2 у точці з абсцисою х0 = -2....
ххх87 ххх87  12.05.2021 15:22
1) y = x+5 по модулю2) y = (x-5)в третьей степени ​...
mmmmm30 mmmmm30  12.05.2021 15:21
в прямой треугольной призме стороны основания равны 25 см 29 см и 36 см. Площадь ее полной поверхности равна 1620см². Найти обьем пизмы...
Iryna452 Iryna452  09.12.2020 06:18
4. Решите систему уравнений графическим х; x+2y=1...
kira309 kira309  09.12.2020 06:18
Y = 4x² функциясының графигін сыз нужно ​...
vitalikkislov vitalikkislov  09.12.2020 06:18
сколько из 10 человек можно выбрать - а) руководителя собрания и прокотолиста ; б) двух представителей . надо решение а и б , то есть 2 решения ....
dju3 dju3  09.12.2020 06:19
X в третьей степени Y во второй степени + Y =...
nastycherry1 nastycherry1  09.12.2020 06:19
Спростіть вираз (x+2)-(x-3)(x+3)Поставлю ​...

Популярные вопросы