Найдите сумму всех натуральных значений n, удовлетворяющих неравенству n^2(n^2 - n - 6) ≤ 0
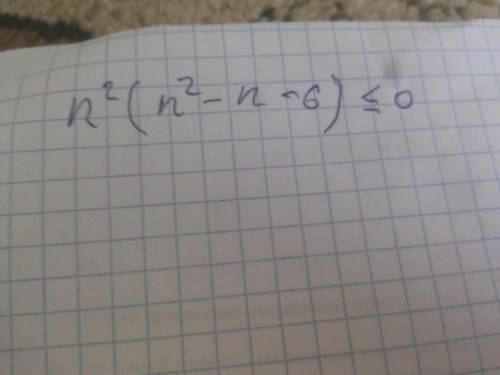
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычисли: 3м8дм+6м2дм-7м7дм= 5дм2см-19см+3дм6см+3дм1см=...
3 - Что обозначает выражение лезть из кожи вон...
3 - Решит ребро одного куба равно 10сантиметрам а другого в 2раза больше. вычисли...
3 - Морфологический разбор слова рождения...
1 - Выпишите из списка отдельно формулы оксидов, оснований, кислот, солей. дайте...
3 - Как произносится слово litte и creatures...
1 - Выражения а) 5х+3у-2х-9у б)2(3а-4)+5 в) 3а-2а-4+а+1 г) 4(3b+2)-2(2b-3) 2. решите...
2 - Как будет переводиться предложение по : мы собираем подарки всем нашим друзьям...
3 - Примеры крупных природных объектов расположенных в южном и северном полушариях...
1 - Make the sentences in exercise 3 negative. use doesn t, don t, isn t or aren...
1
n²(n² - n - 6) ≤ 0
n²(n - 3)(n + 2) ≤ 0
+ - - +
[-2][0][3] n
n ∈ [- 2 , 3]
Натуральные числа принадлежащие этому отрезку : 1 ; 2 и 3 .
1 + 2 + 3 = 6
ответ : 6
n²(n²-n-6)≤0
найдем корни левой части.
n=0; по Виету n=3: n=-2.
-203
+ - - +
х∈[-2;3], сумма натуральных, входящих в ответ , 1+2+3=6