1. Алгебра
  2. Найдите сумму всех четных двузначных

Найдите сумму всех четных двузначных чисел

Lora20060 Lora20060    2   22.05.2019 10:00    4

Ответы
Aksa2101 Aksa2101  17.06.2020 15:58

Запишем члены этого ряда

10, 12, 14, ......., 96, 98

Первый член ряда a₁ = 10

Второй член ряда a₂ = 12 и так далее.

Последний член ряда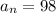 a_n=98

Очевидно что данная последовательность представляет собой

арифметическую прогрессию, так как каждое число начинаемое со второго 12,14,....,96,98 образовано из предыдущего числа добавлением к нему шага прогрессии(равного 2)

Так 12 = 10 + 2, 14 = 12 + 2,....., 98 = 96 + 2

Определим шаг или разность прогрессии - d

d = a₂ - a₁ = 12 - 10 = 2

и количество ее членов прогрессии n из формулы

                       a_n=a_1+d(n-1)

                      n=\frac{1}{d}\cdot(a_n-a_1+d)=\frac{1}{2}\cdot(98-10+2)=\frac{90}{2}=45

Найдем сумму n членов арифметической прогрессии

                         а₁ = 10,   d = 2,     n = 45

по формуле

S =\frac{a_1+a_n}{2}\cdot n = \frac{10+98}{2}\cdot 45 = 2430

 ответ: 2430

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
romanova385 romanova385  17.07.2019 02:50
Построить график функции y=-6/x. с графика найдите а) значение функции, если аргумент равен-1; 1,5; 6 б)значение аргумента,при которых значение функций равно 2 в) значение аргумента...
mksmsslvp0b481 mksmsslvp0b481  17.07.2019 02:50
Выражение: -4)(4+а) б). (5х+у)(у-5х); в). (1-х^3 )(1+x^3 ) г). (2x^2++х) 2. разложить на множители: а). 49-x^2; б). -0,01x^2+у^2; в). 9-а^4; г). -0,04x^2+у^2 z^2 д). (х-1)^2-9....
Zeerorrrrrr Zeerorrrrrr  17.07.2019 02:50
Выразите а-с и с-а через х и у если х= а-b ,у=b-с...
ketivolkowa ketivolkowa  15.03.2021 14:11
3. Упростите и найдите значение выражения:(х+1)(х^2 - x+ 1) — х(х+3)(х – 3), при х = 1,5​...
vladajoyful vladajoyful  15.03.2021 14:11
Высоту над землей подброшенного вертикально вверх мяча вычисляют по формуле h(t) = –2t² + 10t, где h — высота в метрах , t — время в секундах с момента броска. а) Через сколько...
M4KAR M4KAR  15.03.2021 14:11
Высоту над землей подброшенного вертикально вверх камня вычисляют по формуле h(t) = -5t 2 + 16t, где h — высота в метрах, t — время в секундах с момента броска. а) Через сколько...
AnnPogodina1 AnnPogodina1  15.03.2021 14:12
Скажите на многочлены а)2³а- 54б)16х²-8у+у²+8х-2у в)а²-2аб+б²+3а-3б У МЕНЯ СОЧ​...
сема891 сема891  15.03.2021 14:12
Областю визначення якої з наведенних функції є всі числа крім -3 А y= 1_x2+3 Б y= 3_x В y= 1_3+x Г y=1_3x Ці риски дроби...
Заяц699 Заяц699  15.03.2021 14:12
Дана квадратичная функция вида у- х? + 2х 3. Постройте ее график и найдите: a) ось симметрии и промежутки возрастания и убывания: б) координату точки пересечения графика функции...
ryabchenko20021 ryabchenko20021  11.06.2019 00:10
Найдите значение выражения: 3,5*6,8+3,5*3,2; 12,4*14,3-12,4*4,3....

Популярные вопросы