Найдите сумму возможных натуральных значений k, при которых график функции
будет таким, как на
рисунке. (на рисунке изображена ветвь параболы, находящаяся в 1 четверти координат)

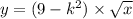
$y = (9 - {k}^{2}) \times \sqrt{x}$

zakriev767 2 08.03.2021 11:46 0

Question

Алгебра: Найдите сумму возможных натуральных значений k, при которых график функции будет таким, как нарисунке. (на рисунке изображена ветвь параболы, находящаяся в 1 четверти координат)​

zakriev767 · Answer

График указанной функции представляет из себя график функции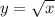 , растянутый или сжатый в зависимости от модуля коэффициента перед корнем, и отраженный симетрично оси х в случае, если коэффициент перед корнем отрицательный.По условию график расположен в 1 четверти. Но и график исходной функции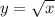 также расположен в 1 четверти. Значит, коэффициент перед корнем - положительный:Натуральных чисел, попавших в полученный промежуток - два: 1 и 2. Их сумма равна 1+2=3.ответ: 3...

Популярные вопросы