Найдите сумму:

и

тема: прогрессия.сумма n первых членов прогрессии. 9 класс
я ничего не поняла.
Другие вопросы по теме Алгебра
Популярные вопросы
- Сделать краткий доклад на тему: Неформальные молодёжные движения,...
2 - Накресли прямий кут по клітинках. Накресли чотири ки МРКО, ВМАС,...
2 - Таблицу Общие сведения о природе Ю.Аи заполнить: климат и внутр....
2 - ОТВЕТЬТЕ НА ВОПРОСЫ 1.Ist Mode fur dich wichtig?2.Was tragst du gerne...
3 - Князівські чвари робили русь-україну слобкою перед зовнішніми загрозами...
1 - Расстояние между городами A և B - 45 км. 2 велосипедиста отправились...
1 - Уровень АЛента машины Тьюринга содержит последовательность символов...
3 - Read the first part of the text and fill in the gaps with the following...
2 - Знайти похідну функцій: 1. = 8 5 + 3 − 5 2. = + 5 3. = 12 + 8 3 −...
2 - Составить схемы взаимодействия природных компонентов по каждой природной...
2
Для нахождения суммы геометрической прогрессии можно воспользоваться формулой: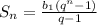 , где
, где 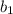 - первый член прогрессии,
- первый член прогрессии, 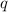 - знаменатель прогрессии,
- знаменатель прогрессии, 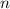 - количество членов в сумме.
- количество членов в сумме.
1)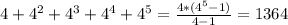
2)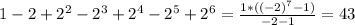
1)
2)