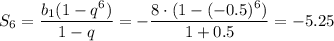Найдите сумму шести первых членов прогрессии, если b2=4; b4=1
Другие вопросы по теме Алгебра
Популярные вопросы
- 3) przedstaw zasady postępowania podczas katastrofy komunikacyjnej...
2 - Уявіть, що ви геолог і вам необхідно знайти родовища кам яного вугілля України...
1 - Подготовка сырья для производства шоколада, ШОКОЛАДНЫХ изделий. ПРОПИСАТЬ...
3 - Произведение Муму перескажите кратко событие где барыня устраивает судьбу...
2 - у меня соч 1/3(3а+9)-1/2(6б-4)=упрости выражение , и найдите его значение...
3 - Complete the sentences using the words from the text. Write only one word....
1 - Задание 2. Прочитайте отрывок из рассказа Л.Толстого «Кавказский пленник»...
1 - Согласно статистическим данным АО «Казгидромет», показатели температуры воздуха...
3 - В каком году Моде заключил мирный договор а)198 б)196 в)199 с)197В каком...
1 - Берілген қанатты сөздерден негізгі ойды анықтаңдар....
2
Знаменатель геометрической прогрессии:
Найдем сумму первых шести членов геометрической прогрессии
Для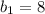 и q=0.5:
и q=0.5: 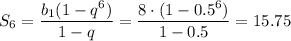
Для и q=-0.5:
и q=-0.5: