Найдите сумму пяти первых членов прогрессии, если b5=81 и b3=36
Другие вопросы по теме Алгебра
Популярные вопросы
- Таня, саша и витя начертили прямой, острый и тупой углы, по одному...
3 - Нужна разложить числа на множители и найди их нок и нод 1)360,588....
3 - Решить ! у ромы в кармане три купюры: 5грн,2грн и 1грн.в магазине он...
1 - Впараллелограме авсд бессектриса угла в пересекает сторону ад в точке...
1 - Распространить предложения второстепенными членами.звонок.кученики...
2 - Как правильно написать точно-точный а колючий как?...
1 - Подобрать однокорреные словам непрозноимым согланым чуство праздник...
3 - Скаким веществом не взаимодействует оксид углерода (iv) а) с оксидом...
3 - Флакон шампуня стоит 190руб .какое наиболь число флакона можно купить...
1 - Вставте пропушеные сказуемые запишите стихтворение. лес зелёным: осень...
2
Найти:
Решение:
Вычислим знаменатель геометрической прогрессии:
Первый член геометрической прогрессии можно вычислить так:
Cумма первых
Вычислим сумму первых
1) Для
2) Для
Найдите сумму пяти первых членов геометрической прогрессии, если b₅ = 81 и b₃ = 36.
Тогда:
b₅ = b₃ * q²
81 = 36 * q²
q² = 81/36
q = ± √(81/36)
q = ± 3/2 = ± 1,5
b₁ = b₃/q² = 36 : (9/4) = 36 × 4/9 = 16
Формула суммы первых n членов геометрической прогрессии:
ответ: 211 и 55
S₅=55 или S₅=211
Объяснение:
Формула нахождения n-члена геометрической прогрессии через первый член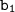 и знаменатель q имеет вид:
и знаменатель q имеет вид:
Тогда из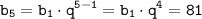 и
и 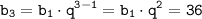 получим:
получим:
Формула суммы первых n-членов геометрической прогрессии через первый член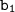 и знаменатель q имеет вид:
и знаменатель q имеет вид:
На основе известных данных получим.
a) q=-1,5:
b) q= 1,5: