1. Алгебра
  2. Найдите сумму первых

Найдите сумму первых пяти членов прогрессии, третий член которой равен 3, а пятый равен 27

маринапашко2000 маринапашко2000    1   19.05.2019 05:30    0

Ответы
syltanchik1338 syltanchik1338  12.06.2020 10:17

найдем четвертый член геометрической прогрессии:

b_{4} = \sqrt{b_{3} * b_{5}

b_{4} = 9

знаменатель прогресси: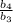 \frac{b_{4}}{b_{3}} = 3

 

первый член прогрессии: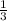 \frac{1}{3}

 

тогда сумма равна: 

 

S_{5} = \frac{b_{1}*(q^{5}-1)}{q-1}

 

S_{5} = \frac{\frac{1}{3} * (3^{5}-1)}{3-1}

 

S_{5} = \frac{\frac{1}{3}*242}{2}

 

S_{5} = \frac{121}{3} = 40\frac{1}{3}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
green151 green151  03.06.2019 09:55
F(x)=1/3sin3x-1/3x найти работы фракции умоляюю...
KatyaD2005 KatyaD2005  03.06.2019 10:50
Как изменятся значения sinα, cosα, tgα,ctgα если угол α будет возрастать от π/2 до π...
АнонАнонимовиччч АнонАнонимовиччч  03.06.2019 10:50
(х^2-1)(х^2+1)(x^4+1)(x^8+1) - в многочлен...
Натальяроссия Натальяроссия  03.06.2019 09:46
Исследуйте функцию.f(x)=(x-+4) и постройте её график....
munisa333 munisa333  03.06.2019 09:40
Два автомобиля выезжают одновременно из одного города в другой скорость первого на 20км/час больше скорости другого поэтому первый автомобиль приезжает на место на 3ч 30мин раньше...
kazhizhanov kazhizhanov  03.06.2019 09:34
Тело движется по прямой со скоростью v(t)=(4t+2) м/с. найдите длину пути , пройденного телом за 3 секунды от начала движения....
ogannisyan2006 ogannisyan2006  03.06.2019 09:25
Задайте примеры с буквенные выражение с дробями (7 класса )...
sladkoegka03 sladkoegka03  03.06.2019 09:25
На рисунке график квадратичной функции (а=1) по графику определите 1) координаты вершины параболы 1...
igor331 igor331  15.09.2019 12:10
Решить (8*х+10)(3-х)=(11-8*х)(4*х+5)-5...
spanielskubidu1 spanielskubidu1  15.09.2019 12:10
Выражение: (x-2)(x-11)-2x(4-3x) a) 7x в квадрате -21 x-22 b) 7x в квадрате +21x+22 c) 7x в квадрате +21x-22 d)-7x в квадрате +21x+22 e) 7x в квадрате -21x+22 умоляюю...

Популярные вопросы