Найдите сумму коэффициентов a и b кубического многочлена х^3+ax^2+bx+3 , имеющего три различных корня, два

Question

Алгебра: Найдите сумму коэффициентов a и b кубического многочлена х^3+ax^2+bx+3 , имеющего три различных корня, два из которых являются корнями квадратного трехчлена x^2+2x-1 .

SomaHin · Answer

Представим данное выражение в виде разложения на множителигде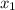 — неизвестный корень. ТогдаПриравниваем коэффициенты при степени xСумма коэффициентов a и b: -1 + (-7) = -8ответ: -8....

Найдите сумму коэффициентов a и b кубического многочлена х^3+ax^2+bx+3 , имеющего три различных корня, два из которых являются корнями квадратного трехчлена x^2+2x-1 .

Популярные вопросы