1. Алгебра
  2. Найдите сумму четвёртых

Найдите сумму четвёртых степеней корней уравнения x^2+x-1=0

Maowsk Maowsk    3   05.06.2019 00:34    2

Ответы
daramalahova907 daramalahova907  05.07.2020 18:54

Обратим сразу внимание на то, что уравнение имеет два корня. Для этого или посчитаем дискриминант, или заметим, что график функции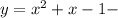 y=x^2+x-1 - парабола, ветви которой направлены вверх, причем y(0)=-1<0, что гарантирует два пересечения этой параболы с осью OX (координаты точек пересечения и являются корнями уравнения).

1-й По теореме Виета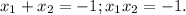 x_1+x_2=-1; x_1x_2=-1.

Далее,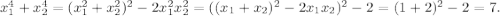 x_1^4+x_2^4=(x_1^2+x_2^2)^2-2x_1^2x_2^2=((x_1+x_2)^2-2x_1x_2)^2-2=(1+2)^2-2=7.

2-й Если x - корень уравнения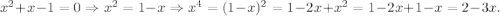 x^2+x-1=0\Rightarrow x^2=1-x\Rightarrow x^4=(1-x)^2=1-2x+x^2=1-2x+1-x=2-3x.

Таким образом,

x_1^4=2-3x_1;\ x_2^4=2-3x_2; x_1^4+x_2^4=2-3x_1+2-3x_2=4-3(x_1+x_2)=4+3=7

ответ: 7

ПОКАЗАТЬ ОТВЕТЫ
annykovaleva annykovaleva  05.07.2020 18:54

{x}^{2} + x - 1 = 0

По теореме Виета

x1 + x2 = - 1 \\ x1 x2 = - 1

Нам надо вот такое:

{x1}^{4} + {x2}^{4} = ( {x1}^{2} + {x2}^{2} )^{2} - 2 {(x1x2)}^{2} = ({(x1 + x2)}^{2} - 2 {(x1x2)}^{2})^{2} - 2x1x2 = (1 + 2)^2 - 2 =9-2=7

ответ: 7

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
andreymarshev0p0b1aa andreymarshev0p0b1aa  20.11.2021 09:16
Решите систему уравнений МЕТОДОМ ПОДСТАНОВКИ...
anastasialishcnastya anastasialishcnastya  20.11.2021 09:19
Дам за это Тест на фото. Сделайте хотя бы несколько вопросов...
saidislom01 saidislom01  20.11.2021 09:28
8 класс 1. Упростите выражение: a) b) c) d)15 2. Выполните действие: а) b) c) d) 3.Упростите и найдите значение выражения: a) , если m =, n = -3. b), если x = 2,5; -1. 4....
toniskvortsov1 toniskvortsov1  20.11.2021 09:31
С решением !! Имеется 6 ламп с надежностью 0,75. Какова вероятность того, что не менее пяти из них исправны?...
anya12345678900 anya12345678900  20.11.2021 09:32
ТОчка М - середина отрезка АВ, точка К - середина отрезка МВ. найдите длину отрезка АК,если ВК = 3 см...
Pilots21 Pilots21  20.11.2021 09:35
Периметр треугольника 10,8 дм, нужно найти 3ю сторону треугольника, зная что 1ая сторона в 3 раза больше третьей, а вторая на 2,6 меньше чем 3я сторона...
льоха7 льоха7  12.05.2020 17:29
Машина 3/5 м ткани обработает за 2 4/25 мин сколько требуется времени чтобы обработать 1 1/4 м такой ткани​...
птмпль птмпль  12.05.2020 17:23
Найдите угловой коэффициент касательной к графику функции f ( x) = 2x^3-3x^2 + x в точке с абсциссой x0=1 Решение расписывать...
muss07 muss07  12.05.2020 17:22
Составьте какую нибудь систему двух линейных уравнений с двумя переменными, решением которой является пара значений переменных: З=6,y=0...
5675566 5675566  04.04.2020 19:52
Вкладчик поместил в банк 1067 р. Банк ежегодно выплачивает вкладчику 4% от суммы вклада. Какую сумму денег получит вкладчик через 2 года? (Промежуточные вычисления округляй...

Популярные вопросы