Найдите сумму целых корней уравнения: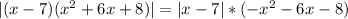 (ответ:-2)

ответ: -2

Объяснение:

Поскольку левая часть уравнения неотрицательна, то раз |x-7| в правой части неотрицательно, то -(x^2+6x+8) >= 0

При выполнении этого условия, данное уравнение из свойства модуля равносильно следующему:

|(x-7)(x^2+6x+8)| = |(x-7)*(- (x^2+6x+8))|

|(x-7)(x^2+6x+8)| = |(x-7)(x^2+6x+8)|

Иначе говоря, уравнение обращается в тождество, а значит решения этого уравнения эквивалентны всем решениям неравенства:

-(x^2+6x+8) >= 0

+ решение x= 7

x^2 +6x + 8 <=0

(x+4)(x+2) <=0

x∈[-4; - 2]

Тогда сумма целых решений:

s= (-4)+ (-3) + (-2) + 7 = -2