1. Алгебра
  2. Найдите среднее арифметическое

Найдите среднее арифметическое целых корней уравнения: 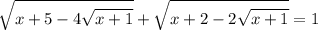\displaystyle \sqrt{x+5-4\sqrt{x+1} } + \sqrt{x+2-2\sqrt{x+1} } =1

RoadGoodGame RoadGoodGame    1   18.03.2021 23:53    0

Ответы
викусик152 викусик152  18.04.2021 00:05

\displaystyle \sqrt{x+5-4\sqrt{x+1}}+\sqrt{x+2-2\sqrt{x+1}}=1\\\\ODZ: x\geq -1\\\\\sqrt{x+1}=t; t\geq 0\\\\x+1=t^2\\\\x=t^2-1\\\\\sqrt{t^2-1+5-4t}+\sqrt{t^2-1+2-2t}=1\\\\\sqrt{(t-2)^2}+\sqrt{(t-1)^2}=1\\\\|t-2|+|t-1|=1\\\\0\leq t\leq 1\\\\2-t+1-t=1\\\\3-2t=1\\\\t=1

подходит под условие, тогда обратная замена

\displaystyle \sqrt{x+1}=1\\\\x+1=1\\\\x=0

\displaystyle 1

истина. тогда подходят все t из промежутка (1;2]

обратная замена

\displaystyle 1

\displaystyle t2\\\\t-2+t-1=1\\\\2t=4\\\\t=2

по условию не подходит т.к. t>2

тогда общее решение x=0 или x∈(0;3]. Значит объединение [0;3]

целые корни уравнение 0+1+2+3=6

среднее арифметическое 6/4=1,5

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
misakimei1306 misakimei1306  21.05.2019 23:50
Решите ,7к=11,4 0,001н=-2; 3(0,4-х)=9; 0,2(х-7)=0,8;...
Анастасия126783 Анастасия126783  21.05.2019 23:50
Чашка, которая стоила 90 рублей, продаётся с 10% скидкой. при покупки 10 таких чашек, покупатель отдал кассиру 1000 рублей.сколько рублей сдачи он должен получить? ( )...
kainkem kainkem  21.05.2019 23:50
Вкакой точке нужно провести касательную к графику функции y=x+3/x , чтобы она пересекала ось ординат в точке (0; 3) заранее ))...
TEMA3232 TEMA3232  21.05.2019 23:50
Может ли выражение: а) а2+16а+64 принимать отрицательные значения. б) -б2-25+10б принимать положительные значения в) -х2+6х-9 принимать неотрицательные значения г) (у+10)2-0.1...
hudo1 hudo1  21.05.2019 23:50
)одночлены к стандартному виду: a)-4b*0,25b^4 b)-5x y^3 (-2x^3 y)^2 c) (3x^2 y)^2 d) 2b^2*(-a^2 b)^3...
вжух8 вжух8  21.05.2019 23:50
Решите . в треугольнике abc каждая сторона равна 5 см,а в треугольнике mnp каждая сторона равна 10 см. найдите отношение периметра dabc к периметру dmnp?...
Anastasia6226 Anastasia6226  21.05.2019 23:50
Выполните действия: 2a^2b(-3ab^2)^2...
Vikakotik5 Vikakotik5  21.05.2019 23:50
Первый рабочий изготавливает за час на 2 детали больше,чем второй.первый рабочий работал 10 ч, а второй - 20 ч . вместе они изготовили 320 деталей. составьте уровнение для нахождения...
Ramires01 Ramires01  21.05.2019 23:50
Составьте предложения , используя глаголы условного наклонения с частицей бы на темы в нашем классе...
scream75821 scream75821  21.05.2019 23:50
Докажи,что среди восьми различных натуральных чисел,найдутся хотя бы два числа,разность которых делится на 7...

Популярные вопросы