Найдите sin236* если sin28*=a
Другие вопросы по теме Алгебра
Популярные вопросы
- Рассчитайте начисленную заработную плату педагогического работника, если выплаченная...
1 - Уже в 1931 г. секретным решением НКВД ограничивались гонения на беспартийных...
2 - Read the text. Then write true or false. Correct the false sentences. (10...
3 - 1. Соотнесите группы животных с их особенностями строения выделительной системы:...
2 - Одна пятая от 100 (если что это дробь чисто дробь без добавок)...
3 - Укоротите(сожмите) текст. В повести Максима Горького «Детство» множество эпизодов,...
1 - Вопросы и задания 1. На физической карте Узбекистана определите географическое...
2 - Диаметр первого Круга такой же как радиус второго Круга если радиус первой...
3 - Уровень и динамика развития отраслей сельского хозяйства...
3 - 1. Прочитайте текст и ответьте на вопросы. Текст:Открытые Колумбом новые земли...
3
5)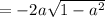
Объяснение:
так как 0<28<90 - то косинус положителен
Объяснение:
sin236=sin(180+56)=-sin56, ( формула: sin2a=2sina*cosa) =
-2sin28*cos28=-2*a*cos28= (формула: cos^2a=1-sin^2a) =
-2*a*V(1-a^2), (1-a^2 стоит под корнем V )