Найдите рациональные корни многочлена и классифицируйте его на множители. 5x^(5)-8x^(4)+46x^(3)+21x^(2)-21x+3
Другие вопросы по теме Алгебра
Популярные вопросы
- Материк, крайние точки которого находятся в четырех полушариях...
1 - Масштаб, наиболее подходящий для полярной съемки...
2 - Массив Хан-Тенгри находится в горах...
2 - Малоазиатское, Армянское и Иранское нагорья образуют...
1 - Максимальная глубина Индийского океана...
3 - Масштаб 1:5000000, на карте между двумя точками расстояние 2 см, то чему...
2 - Максимум осадков на казахстанской части Западно-Сибирской равнины (до 60%)...
3 - Массовый падеж скота, связанный с климатом...
2 - Масштаб 1:10000. переведите в именованный масштаб...
3 - Маршрутная съемка местности - это...
2
(см. объяснение)
Объяснение:
Т.к. ваш предыдущий вопрос был удален странным модератором, а я на него написал ответ, то даю ответ на тот вопрос в этом:
Понятно, что первые два корня - это 3 и -2.
Решим уравнение:
По тригонометрической теореме Виета:
Т.к.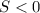 и
и 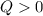 , то:
, то:
Тогда:
Уравнение решено!