1. Алгебра
  2. Найдите промежутки знакопостоянства

Найдите промежутки знакопостоянства функции y=x^3-2x^2-8x/x^2-1 y=x^2-9/x^2-4 y=x^2+4/x^2+3x хотя бы одно ! )

egorsh1 egorsh1    3   06.09.2019 22:10    0

Ответы
bertain bertain  03.08.2020 20:46
Числовые промежутки, на которых функция сохраняет свой знак (т.е. остается положительной или отрицательной), называются промежутками знакопостоянства функции.

1)\; \; y=\frac{x^3-2x^2-8x}{x^2-1} \\\\y=0\; \to \; \left \{ {{x^3-2x^2-8x=0} \atop {x^2-1\ne 0}} \right. \; \left \{ {{x(x^2-2x-8)=0} \atop {(x-1)(x+1)\ne 0}} \right. \; \left \{ {{x(x-4)(x+2)=0} \atop {x\ne -1,\; x\ne 1}} \right. \\\\---[-2\, ]+++(-1)---[\, 0\, ]+++(1)---[\, 4\, ]+++\\\\y\ \textgreater \ 0:\; \; x\in (-2,-1)\cupc(0,1)\cup (4,+\infty )\\\\y\ \textless \ 0:\; \; x\in (-\infty ,-2)\cup (-1,0)\cup (1,4)

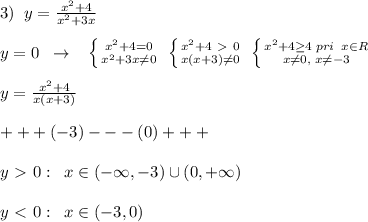
3)\; \; y= \frac{x^2+4}{x^2+3x} \\\\y=0\; \; \to \; \; \; \left \{ {{x^2+4=0} \atop {x^2+3x\ne 0}} \right. \; \left \{ {{x^2+4\ \textgreater \ 0} \atop {x(x+3)\ne 0}} \right. \; \left \{ {{x^2+4 \geq 4\; pri\; \; x\in R} \atop {x\ne 0,\; x\ne -3}} \right. \\\\y= \frac{x^2+4}{x(x+3)} \\\\+++(-3)---(0)+++\\\\y\ \textgreater \ 0:\; \; x\in (-\infty ,-3)\cup (0,+\infty )\\\\y\ \textless \ 0:\; \; x\in (-3,0)
ПОКАЗАТЬ ОТВЕТЫ
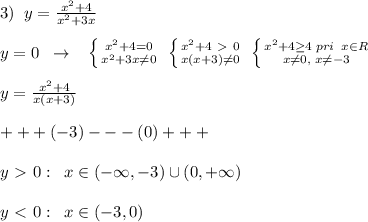
Другие вопросы по теме Алгебра
DzhabbarovaS DzhabbarovaS  09.03.2019 00:20
2тракториста за 7 дней вспахали 147га земли площадь земли вспаханной 1трактористом за 3 дня равна площади земли вспаханной земли 2 за 4 дня сколько впахал каждый за...
ДмитрийJ ДмитрийJ  09.03.2019 00:10
Разность двух чисел равна 5 ,найдите эти числа ,если 2/9 меньшего из них равны 20% большего...
Змей19 Змей19  09.03.2019 00:10
:) укажите выражение, равное 3^2k-1 ; a) 3^2k - 3; 2k корень b) (3^2k)^-1 c) 9^k/3 d) 3^2k / 3^-1...
polina2004121 polina2004121  09.03.2019 00:10
Найти max и min функции: y = 2 sin x + cos 2x...
vlad499999 vlad499999  09.03.2019 00:10
Если серёжа потратит 7.5% имеющихся у него денег,то у него останется 101 рубль 75 копеек.сколько денег у серёжи?...
agadoraaa agadoraaa  09.03.2019 00:10
Обчисліть площу фігури , обмеженоі лініями а) ігрик дорівнює корень з ікса,ігрик дорівнює ікс....
ivanovali0109 ivanovali0109  09.03.2019 00:10
Разложите на множители многочлен: а)9х^2 + 6xy + y^2 - z^2 б) 16a - 16b - a^3 + a^2b...
kanumah2 kanumah2  04.08.2019 13:59
Решить уравнение с разложения на множители: x-2/x^3=2x-x^2...
gaifuling4owmrcy gaifuling4owmrcy  04.08.2019 15:10
Решите уравнение: а) -3х-1=0 объясните, как вы это сделали...
lisovak0777 lisovak0777  04.08.2019 13:13
Выразите скорость света с м/с; запишите результат, используя степень числа 10...

Популярные вопросы