1. Алгебра
  2. Найдите промежутки знакопостоянства

Найдите промежутки знакопостоянства функции y=3x-x^2

vladikpadic vladikpadic    3   17.12.2019 21:10    14

Ответы
AbraevAidar AbraevAidar  10.10.2020 21:19
Решение:Промежутки знакопостоянства - это промежутки, на которых значение функции не меняет свой знак.

Заметим, что графиком функции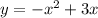 y=-x^2 + 3x будет являться парабола, ветви которой направлены вниз (так как 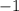-1 - коэффициент при 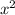x^2 меньше ноля).

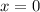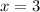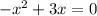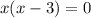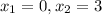Пересечения оси абсцисс и графика рассматриваемой функции будут достигаться при x=0 и x=3 (как решения уравнения -x^2 + 3x = 0, x(x-3)=0, x_1=0, x_2=3).

Значит, можно выделить следующие промежутки знакопостоянства функции:

при x \in ( - \infty; 0 ) значение функции меньше ноля;при x \in (0;3) значение функции больше ноля;при x \in (3; + \infty ) значение функции меньше ноля.

График "с доказательством" в приложении.

ответ: ( - \infty; 0), (0;3), (3; + \infty ).
Найдите промежутки знакопостоянства функции y=3x-x^2
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Mitaren10n3 Mitaren10n3  23.05.2021 18:07
ОТВЕТ , НАПЕЧАТАЙТЕ! А НЕ СФОТКАЙТЕ...
Arabovih1975 Arabovih1975  23.05.2021 17:59
Побудуйте графік функції у = х^2 – 4x — 5. Користуючись графіком, знайдіть проміжок, на якому функція зростає....
машабудьтедобр машабудьтедобр  17.12.2019 16:07
Решите уравнение графическим методом; )...
lasalina lasalina  17.12.2019 16:06
Избавиться от ирациональных чисел...
iruna4 iruna4  17.12.2019 16:03
Абсолютная или условная сходимость...
ashatsejtenov ashatsejtenov  17.12.2019 16:03
Графік функцій -8/x=-2x без рисунка...
sayfulloevo sayfulloevo  17.12.2019 16:02
Решите неравенства[tex]x \times (0.5)^{x} \geqslant - 8[/tex][tex]2 ^{x^2 - 4x + 5} \geqslant 4x - 2 - x {}^{2} [/tex]​...
Ivan856IgR Ivan856IgR  17.12.2019 16:02
Найти приближенное значение корень из 10 округлить полученное значение до сотых...
ник5044 ник5044  26.05.2020 11:17
Какой из данных ответов верный?))) ​...
Tolganay11 Tolganay11  26.05.2020 11:17
Написать уравнение касательной к графику функции f (x) = х ³ - 2х² + 8 х - 3, в точке х 0 = 2....

Популярные вопросы