Найдите промежутки возрастания и убывания функций (через производную решается): 1)f(x)=x^3/3 + 5x^2/2 + 7x + 1 2)f(x)=2x^3-3x^2-12x-1 3)g(x)=sinx + 2 x + 1 (решение опишите подробно)

Ответы

Света20177 11.06.2020 21:27

Решается с приравнивания производной к нулю и нахождения корня

$f(x)=\frac{x^3}{3}+\frac{5x^2}{2}+7x+1\\ f'(x)=x^2+5x+7\\ x^2+5x+7=0\\ D=25-4*7=-3\\ \o$

нет корней, это обозначает, что на все отрезке функция либо убывает, либо возрастает.

смотрит на знак старшей степени функции $\frac{x^3}{3}$ положительный, значит функция возростающая.

$(-\infty;+\infty)$ - промежуток возрастания

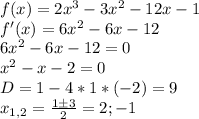
2) $f(x)=2x^3-3x^2-12x-1\\ f'(x)=6x^2-6x-12\\ 6x^2-6x-12=0\\ x^2-x-2=0\\ D=1-4*1*(-2)=9\\ x_{1,2}=\frac{1\pm 3}{2}=2;-1\\$

отмечаем точки на интервале и расставляем знаки начиная с плюса, т.к. у производной у "x"-а старшей степени положительный знак

_+_(-1)_-_(2)_+_

Интервалы с плюсами - возрастание

интевал с минусом - убывание

$(-\infty;-1)\cup(2;+\infty)$ - промежутки возрастания

(-1;2) - промежуток убывания

$g(x)=sinx+2x+1\\ g'(x)=cosx+2\\ cosx+2=0\\ cosx=-2\\ \o$

косинус не может быть меньше -1 и больше 1.

значит функция либо возрастает, либо убывает на всем промежутке

лучше её для этого построить и посмотреть. но и по положительному знаку "x"-а видно, что она возрастающая.

$(-\infty;+\infty)$ - промежуток возрастания

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Алгебра

vaniafatyanov 28.04.2020 02:52

teodor16090 28.04.2020 03:12

cvetaharlanova 28.04.2020 03:12

aydarsadikov 28.04.2020 03:12

tetyanaostafi 19.06.2019 18:00

darkishlord 19.06.2019 18:00

елена1170 19.06.2019 18:00

Kalimovnadir 19.06.2019 18:00

Níkiskastarling28 19.06.2019 18:00

Проверить функцию на четность у = 3x...

Mark786 19.06.2019 18:00