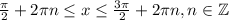Найдите промежутки возрастания и убывания функции: 1) f{x)=x⁴-2x² 2) f{x)=sinx
Другие вопросы по теме Алгебра
Популярные вопросы
- ответьте на вопросы по рассказу максима горького челкаш : 1.какие ощущения вызвал...
1 - 1)южную америку так же,как ми африку, той лишь разницей, этого следует,что южная...
3 - Составьте предложения.i would like to составьте предложения. i would like to...
2 - Предприниматель получил 10 000 руб. прибыли. налог на прибыль-30%. сколько рублей...
2 - Дибромзамещенный алкан содержит 85 , 1 % брома . определите формулу дибромалкана....
2 - Почему обжёгся о ложку в стакане с горячим чаем, хотя держал ее за конец, не...
1 - Решить ! поез проехал 1/6 намеченного маршрута.длина всего маршрута 66 км. сколько...
3 - Обозначьте строчку где пишется нн а) тесто, семена б)суше..ая ягода, суп в)...
3 - Определяй, какими членами предложения являются однородные члены, и подчеркивай...
2 - Прочитай выражение и найди их значение наиболее удобным...
2
1) Найдём производную функции: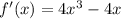
Нули производной: -1; 0; 1.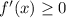 , т. е. функция возрастает при
, т. е. функция возрастает при ![x\in[-1; 0]\cup[1; +\infty)](/tpl/images/0945/9191/f0b43.png) ;
; 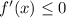 , т. е. функция убывает при
, т. е. функция убывает при ![x\in(-\infty; -1]\cup[0; 1]](/tpl/images/0945/9191/b9b62.png) (см. рис. 1)
(см. рис. 1)
2)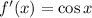
Рассмотрим функцию на тригонометрической окружности (см. рис. 2). При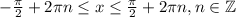
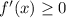 , т. е. функция возрастает; при
, т. е. функция возрастает; при 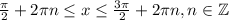
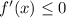 , т. е. функция убывает.
, т. е. функция убывает.
ответ: 1) Возрастает при![x\in[-1; 0]\cup[1; +\infty)](/tpl/images/0945/9191/f0b43.png) , убывает при
, убывает при ![x\in(-\infty; -1]\cup[0; 1]](/tpl/images/0945/9191/b9b62.png) ; 2) Возрастает при
; 2) Возрастает при 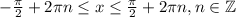 , убывает при
, убывает при