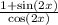
найдите произвольную функции
Другие вопросы по теме Алгебра
Популярные вопросы
- Сделать звуко-буквенный разбор слова высокие ! !...
3 - Запишите в виде десятичной дроби число, в котором : 1) три единицы, четыре десятых,...
3 - На фиранки для викон а м тканини розризали на частини по 3 м кожна. скильки фиранок...
2 - Варифметической прогрессии {an} найдите номер её члена an если а с решением....
2 - Слово (запрягаться)образовано от какого исконно слова? !...
3 - Эхх, плохо у меня с информатикой.. , ) 1. примеры понятий: тождественных, пересикающихся,...
2 - Найти прилогательное + существительное. когда-то в языке слово стол означало место...
3 - Надо окрасить 60 м2 поверхности стены. 75% работы уже сделали. какую площадь осталось...
1 - Найдите слова, в которых написание гласной в корне проверяется ударением. подрости...
1 - Что характерно для степной зоны западной сибири? а )типичные почвы имеют меньшую...
1
Найдём производную данной функции.