1. Алгебра
  2. Найдите производные функций

Найдите производные функций f(x)=cos(3x^2-4x+2) f(x)=sin(2x^2-3x+1) напишите уравнение касательной к графику функции y=f(x),в точку абсциссой,равно x f(x)=x cos x x=пи/2 найдите производную y=f(x) y=6cos^2(5x+4)+ctg)1-6x^2) y=8tg(2+5x^3)-5sin^2(7-8x)

adidok199680 adidok199680    1   24.06.2019 09:50    0

Ответы
vkunney vkunney  19.07.2020 22:28
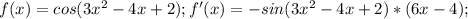
f(x)=cos(3x^2-4x+2);f'(x)=-sin(3x^2-4x+2)*(6x-4);
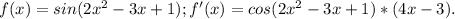
f(x)=sin(2x^2-3x+1); f'(x)=cos(2x^2-3x+1)*(4x-3).

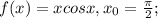
f(x)=x cos x ,x_0= \frac{ \pi }{2};
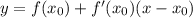y=f(x_0)+ f'(x_0)(x- x_{0}) Это формула уравнения касательной.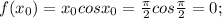
f(x_0)= x_{0}cos x_{0}= \frac{ \pi }{2}cos \frac{ \pi }{2}=0;
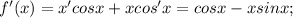
f'(x)=x' cos x+x cos' x=cos x-x sin x;
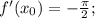
f'(x_0)=-\frac{ \pi }{2};
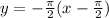
y=-\frac{ \pi }{2}(x-\frac{ \pi }{2})
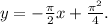
y=-\frac{ \pi }{2}x+\frac{ \pi^2 }{4}.

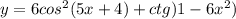
y=6cos^2(5x+4)+ctg)1-6x^2)
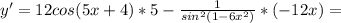
y'=12cos(5x+4)*5- \frac{1}{{sin^2}(1-6x^2)}*(-12x)=
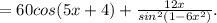
=60cos(5x+4)+ \frac{12x}{{sin^2}(1-6x^2)}.
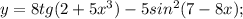
y=8tg(2+5x^3)-5sin^2(7-8x);
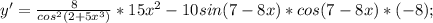
y'= \frac{8}{cos^2(2+5x^3)}*15x ^2-10sin(7-8x)*cos(7-8x)*(-8);
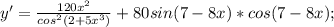
y'= \frac{120x ^2}{cos^2(2+5x^3)}+80sin(7-8x)*cos(7-8x);
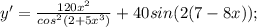
y'= \frac{120x ^2}{cos^2(2+5x^3)}+40sin(2(7-8x));
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
BubbleRise BubbleRise  18.04.2021 05:01
Реши систему:{x=910x−y=11ответ:??? ​...
алеся678 алеся678  18.04.2021 03:18
У коробці лежать 36 карток, пронумерованих числами від 1 до 36. Яка ймовірність того що на навмання взятій картці буде записане число кратне числу 4ні кратне числу 3, ні кратне числу...
MEOWчтательница MEOWчтательница  18.04.2021 03:06
Дано вибірку кількості сонячних днів у кожному місяці протягом двох років 12, 8, 16, 20, 25, 24, 26, 19, 18, 14, 12, 13, 12, 9, 16, 29, 25, 25, 23, 20, 18, 14, 12, 16. Складіть частотну...
nector nector  18.04.2021 03:06
,доказать,что треугольник RMS = треугольнику RNS...
kingofpopmusic kingofpopmusic  18.04.2021 03:05
У фінальній частині чемпіонату Європи з футболу беруть участь 16 команд. Скількома можуть розподілитися - золоті, срібні та бронзові команди ​...
пропин пропин  18.04.2021 02:07
Знайдіть об єднання, перетин і різницю множин А={a,b,c,d,e,f,g} та В={b,d,e,j,k} .​...
rast052 rast052  18.04.2021 01:38
Протягом перших шести днів жовтня температура повітря о 8 годині ранку була такою - 8 град; 10 град; 6 град; 8 град; 9 град; 7 град. Знайти розмах вибірки ОЧЕНЬ .​...
adam83 adam83  27.04.2020 13:24
Представить квадрат двучлена в виде многочлена​...
uncu4ek uncu4ek  27.04.2020 12:45
Розвяжіть рівняння y²+5y/y+1= 6/y+1...
hyperIcum hyperIcum  27.04.2020 12:45
Двоє робітників разом виготовили 460 деталей.Перший працівник трудився 7 днів(і), а другий — 6 днів(і).Скільки деталей виготовляв кожен робітник за один день, якщо другий працівник...

Популярные вопросы