Найдите производную функции !
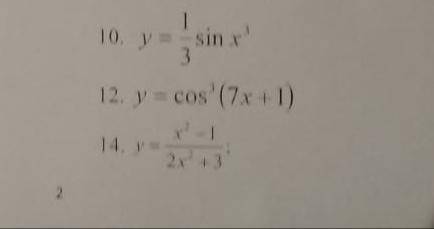
Другие вопросы по теме Алгебра
Популярные вопросы
- (0 Задания по 1. К кому и в какой части стихотворения обращается...
3 - 1 Определите в какой порции и вещества больше молекул: в 33,6 л....
1 - какая сила тока в обмотка электродвигателя,если через них за 0.5...
1 - Махамбеттің азаттық ойлары...
2 - Подставить слова из коробки в пробелы...
3 - очень надо кто разбирается >...
3 - 1.Choose regular comparative adjectives (big, more beautiful, biggest,...
1 - любители русского языка… Задание. Определите часть речи. Укажите...
2 - Мезгіл үстеуін қосып, мәтіннің екі сөйлемін өзгеріп, қайта құра....
1 - РАЗРЕЗАТЬ 1/4 ЧАСТЬ ДЕТАЛИ...
2
Объяснение:
Найдите производную функции
10. y = (1/3)sinx³ ;
12. y = cos³(7x+1) ;
14. y = ( x² -1 )/(2x²+3) .
ответ: 10. x²cosx³ ; 12. - 21cos²(7x+1)*sin(7x+1) ; 14. 10x / (2x²+3)² .
Объяснение:
10.
y ' = ( (1/3)sinx³ ) ' =(1/3)*(sinx³ ) '=(1/3)*(cosx³)*(x³) ' = (1/3)*(cosx³)*3x² =
x²cosx³.
12.
y ' = ( cos³(7x+1) ) ' = 3cos²(7x+1)* ( cos(7x+1) ) ' =
3cos²(7x+1)*( -sin(7x+1 ) *(7x+1) ' = - 3cos²(7x+1)*sin(7x+1 ) *(7*(x)'+1 ') =
- 3cos²(7x+1)*sin(7x+1 )*(7*1+0) = -21cos²(7x+1)sin(7x+1 ) .
14.
y '= ( ( x² -1 )/(2x²+3) ) ' =( (x² -1 )' *(2x²+3) - (x² -1) *(2x²+3) ' ) /(2x²+3)² =
( 2x(2x²+3) - (x² -1) *4x ) /(2x²+3)² = 10x / (2x²+3)².