Найдите произведение всех действительных корней уравнения: 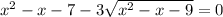
Другие вопросы по теме Алгебра
Популярные вопросы
- Глубина бассейна равна 2 м. ширина-10м. в длина-25м. найдите суммарную площадь боковых...
3 - Смомента открытия, школьная библиотека выписывает для педагогов 24 журнала серии...
2 - 27. das (groß) volksfest weltweit findet jedes jahr in münchen statt: das oktoberfest...
3 - Известно что произношение звуков зависит от того какой у них сосед . подумайте в...
1 - Ателье получило девять рулонов шерстяной ткани,по 36 метров в каждом. из половины...
1 - 1. чем характеризуется биоценоз и фитоценоз? 2. объясните, в чем различие между...
3 - Для легкового автомобиля требуется 9л бензина на 100км пути. сколько литров бензина...
1 - Улены в 4 раза меньше марок, чем у саши, но в 2 раза больше, чем у пети. обозначь...
3 - Если на высоте 3 тысяч.метров термометор показывает 0 градусов.цельсия, то кокова...
3 - Пословицы о дружбе и единстве уральского края....
3
(см. объяснение)
Объяснение:
Замена:
Обратная замена:
Уравнение решено!