Найдите произведение корней уравнения
Другие вопросы по теме Алгебра
Популярные вопросы
- очень . Составить диалог на казахском языке 3 предложения на тему Сарыағаш....
1 - Look at the words in blue in the text and complete the table. Голубые...
1 - Алгебра 10 класс номер 193...
1 - очень надо составить 3 вопроса и 3 ответа очень надо ...
3 - Написать программу(Pascal),нахождение площадей параллелограмма и треугольника...
3 - Визначте відміну і групу іменників:...
2 - Які обмеження автономії Гетьманьщини були здійснені за Петра...
3 - -сабақ Бұл қай мезгіл?1-тапсырма. Өлеңді оқыңдар. Ақынның сөз қолданысына...
2 - с заданием , заранее . Времени разбирать фотографии нет, могла скинуть...
2 - Знову хімія, будь ласка до іть...
2
ОДЗ: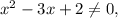
По теореме, обратной теореме Виета
По теореме, обратной теореме Виета
СМ. ДОКУМЕНТ