1. Алгебра
  2. Найдите произведение корней

Найдите произведение корней логарифмического уравнения​

рита2008 рита2008    1   15.06.2019 18:59    0

Ответы
максим1718 максим1718  12.07.2020 20:41
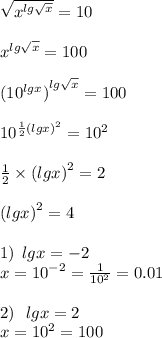\sqrt{{x}^{lg\sqrt{x}}}=10\\\\{x}^{lg\sqrt{x}}=100\\\\{({10}^{lgx})}^{lg\sqrt{x}}=100\\\\{10}^{\frac{1}{2}{(lgx)}^{2}}={10}^{2}\\\\\frac{1}{2}\times{(lgx)}^{2}=2\\\\{(lgx)}^{2}=4\\\\1)\:\:lgx=-2\\x={10}^{-2}=\frac{1}{{10}^{2}}=0.01\\\\2)\:\:\:lgx=2\\x={10}^{2}=100\\\\Проверкой убеждаемся, что обе корни подходят.Произведение корней данного уравнения равно:х₁ • х₂ = 0,01 • 100 = 1ОТВЕТ: 1
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
hamov1408p06m04 hamov1408p06m04  15.07.2019 01:00
(2х-7)²-11(2х-7)+30=0 напишите полностью решите уравнение,используя метод введения новой переменной....
nazfire2003 nazfire2003  15.07.2019 01:00
7класс шаныбеков разложите а виде произведения...
Маргольц Маргольц  15.07.2019 01:00
Найти производные функции f(x)=x^2+x^3...
nataaleksandro2 nataaleksandro2  15.07.2019 01:00
Решить уровнение 2х во 2 степени +3|х|-5=0 за ранее...
lyudmila198604p06n4e lyudmila198604p06n4e  04.10.2019 15:10
Знайдіть найбільше значення функції y=-x2+2x-7...
Nuriza2002 Nuriza2002  04.10.2019 15:10
Постройте график функции у=2^х и у=(1/3)^х и описать их свойства...
SOLA228 SOLA228  04.10.2019 15:10
Какому промежутку принадлежит корень уравнения 2^5x-4=16^x+3 а) (-∞; -16) б) (-16; 0) в) (0; 17) г) (18; +∞)...
hkkk1gonso hkkk1gonso  04.10.2019 13:42
Найдите x если tgx = -√3/3 на участке [-2п; 0]...
lera10211 lera10211  04.10.2019 15:10
Выделив квадрат двучлена, докажите, что при любом значении х квадратный трехчлен х^2-8х + 17 приобретает положительных значений...
Лисана539 Лисана539  04.10.2019 15:10
Решить уравнение: 125*2^4x - 9*20^(x+1) + 64*25^x =0...

Популярные вопросы