Найдите площадь фигуры,ограниченной линиями. y=x^2+6x+10; y=5
Другие вопросы по теме Алгебра
Популярные вопросы
- Решением линейного неравенства является:...
3 - Які основні чинники, що визначають місце країн у міжнародному поділі праці?...
3 - Как выглядит г.о.в.н.о. это я в шутку...
3 - Прочитайте текст. Придумайте название. Запишите текст, вставив пропущенные...
1 - по литературе. ответьте на во Проблематика повести Один день Ивана Денисовича...
3 - Идея для эссе Какой бы я хотела принять закон...
2 - Назовите экологические проблемы Республики Казахстана...
3 - Часть 1 1. В химической реакции CaCl2 + Na2CO3 = CaCO3 + 2NaCl вещество,...
3 - Что изучает информатика? конструкцию компьютера; компьютерные программы;...
3 - Решите ряд химических преобразований.Назовите все вещества и укажите типы...
2
ответ: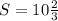 .
.
Объяснение: