Найдите площадь фигуры ограниченной линиям:

Другие вопросы по теме Алгебра
Популярные вопросы
- Как вы считаете, есть ли нечто общее во взглядах на жизнь и роль искусства...
1 - Можете ли вы назвать исторические события, которые повлияли на творчество...
1 - Расскажите об основных принципах марксистского учения....
1 - Выпишите термины параграфа, обозначающие направления и стили художественного...
3 - Объясните утверждения, приведённые в параграфе: «Разрешено всё, что...
2 - Расскажите об изобретении кинематографа....
3 - Объясните причины изменений, которые происходили в положении буржуазии....
2 - В параграфе названо множество имён выдающихся художников и музыкантов...
1 - Выпишите в два столбца: а) термины, характеризующие изменения в процессе...
3 - Кто из названных в параграфе деятелей литературы был активным участником...
1
ответ: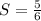 .
.
Объяснение: