1. Алгебра
  2. Найдите площадь фигуры.

Найдите площадь фигуры. (фото). на опечатку не обращайте внимание. (не совпадает с ​

elenaandreeva34 elenaandreeva34    2   19.04.2019 18:07    1

Ответы
KatyaTishkina KatyaTishkina  08.06.2020 01:19

y=1-|x-1|  - "угол" , ветви вниз, вершина в точке (1,1). Можно уравнение этого "угла" расписать на два уравнения :

x\geq 1\; \; \Rightarrow \; \; |x-1|=x-1\; \; \Rightarrow \; \; y=1-(x-1)=-x+2  - это правая ветвь "угла" - прямая,угол наклона к оси ОХ тупой, пересечение с осью ОХ в точке (2,0).

x<1\; \; \Rightarrow \; \; |x-1|=-(x-1)=-x+1\; \; \Rightarrow \; \; y=1-(-x+1)=x - это левая ветвь "угла" - прямая, биссектриса 1 и 3 координатных углов.

Аналогично,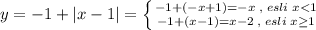  y=-1+|x-1|=\left \{ {{-1+(-x+1)=-x\; ,\; esli\; x<1} \atop {-1+(x-1)=x-2\; ,\; esli\; x\geq 1}} \right.

Проведём ещё прямую х=1, тогда получим треугольник, или слева от х=1, или справа от прямой х=1. Треугольники будут равными, поэтому выбираем любой для подсчёта площади. Я выбираю левый треугольник. Он ограничен прямыми у₁=х , у₂= -х , х=1 . Смотри рисунок.

Основание АВ у треугольника имеет длину 2, высота ОД =1 (видно из чертежа).

Площадь такого треугольника равна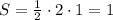 S=\frac{1}{2}\cdot 2\cdot 1=1 .

Через определённый интеграл площадь вычисляется так:

S=\int\limits^a_b\, (y_1(x)-y_2(x))\, dx=\int\limits^1_0\, (x-(-x))\, dx=\int\limits^1_0\, 2x\, dx=\\\\=2\cdot \frac{x^2}{2}\, \Big |_0^1=1^2-0^2=1


Найдите площадь фигуры. (фото). на опечатку не обращайте внимание. (не совпадает с ​
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
leron9999 leron9999  01.10.2019 02:20
Решите уравнение cos6x=0 sin3x=1 ctg2x=-1 tg4x=0...
Aind1 Aind1  01.10.2019 02:20
У=2/3х-1 у=0,4х+2 построить графики функций на одной координатной прямой у=-1/2х+1 у=-3х-3...
DFleX DFleX  01.10.2019 02:30
внести монжитель под знак корня: (х-5)√7...
LILIAGNATIV LILIAGNATIV  01.10.2019 02:30
Для приготовления вишнёвого варенья на 1 кг вишни нужно 2.4 кг сахара в одной упаковке 1 кг сахара сколько упаковок сахара нужно купить чтобы сварить варенье из 17 кг...
antonkovalenko1 antonkovalenko1  05.08.2019 15:30
Группу из 8 человек делят на 2 команды для игры в керлинг.какова вероятность того,что близнецы оля и маша не попадут в одну команду?...
Косинус08111 Косинус08111  05.08.2019 15:30
Решить уравнения 0,2z-0,9=-3,1 -4y-9=-2y-21 3-3(x+8)=-6 -9c-1=41-2c 2x+22=-6x-26 2x+23=15...
ваниль2003 ваниль2003  05.08.2019 15:30
Найдите функцию обратную данной. f (x) = 3/2x - 1 ; y = x в 2 - 4, x 0 y = x в 2 - 4x + 3, x 2 y = корень из 25 - х в квадрате, 0 либо равно х либо равно 5...
indyouk014 indyouk014  05.08.2019 15:30
Сумма вертикальных углов в 2 раза меньше, чем углы им смежные. найдите эти вертикальные углы...
TheBrainPlay TheBrainPlay  05.08.2019 15:30
Как написать сумму числа x и произведение чисел a и b...
Гогенцоллерн Гогенцоллерн  05.08.2019 15:30
7(m+6)-4(3-m)=19 чему равен m,если равенство равно 19...

Популярные вопросы