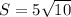Найдите площадь четырёхугольника с вершинами в точках a (–5; –2), b (–1; 1), c (3; –2), d (–1; –4).
Другие вопросы по теме Алгебра
Популярные вопросы
- Какие особенности природы характерны для исландии и гренландии? почему викингов...
1 - 1. состоятельный крот подсчитал, что своими запасами зерна он может целиком заполнить...
2 - Выписать из художественной 4 предложения.с однородными членами и с союзами и без...
3 - Распределить на 2 группы: кислотная. основная. al(oh)3, koh, k2so4, h2so4, hcn,...
3 - Повесть о петре и февронии муромских. как выражено авторское отношение к героям?...
2 - Продолжите в приставках на -з,-с согласными пишется з, а перед с...
1 - Найдите число, 30% которого равны 27...
3 - Какое количество теплоты выделится при кристализации 5 кг алюминия и охлаждении...
2 - Present simple and present continuous test выберите правильный вариант ответа: she...
1 - Найти число, если: 1/3 его равна 30; 1/2 его равна 10; 1/7 его равна 8; 1/8 его...
2
Обозначим два вектора: a=AB и b=AD
1)Найдем координаты ветора a
2)Найдем координаты вектора b
3)Площадь четырехугольника будет являтся модулем векторного произведениея![[a\times b]\\ S=[a \times b] = |a||b| sin(a;b)](/tpl/images/0151/8363/cfe98.png)
Построив,увидим,что четырехугольник - ромб.Соответственно все углы по 45 градусов
4)Найдем модули векторов
5)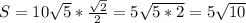
ответ: