1. Алгебра
  2. Найдите первый член

Найдите первый член прогрессии, если сумма её первых s₃=26, а сумма первого и третьего её членов равна 20.

Кактус1313 Кактус1313    1   17.09.2019 07:00    1

Ответы
КаринаМандарина12 КаринаМандарина12  07.10.2020 21:17
Из формулы суммы n первых членов геометрической прогрессии и n-го члена этой же прогрессии, получим систему уравнений

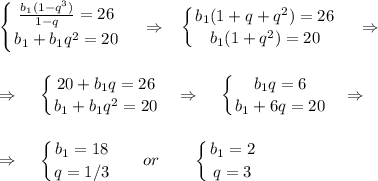
\displaystyle \left \{ {{ \frac{b_1(1-q^3)}{1-q}=26 } \atop {b_1+b_1q^2=20}} \right. ~~~\Rightarrow~~ \left \{ {{b_1(1+q+q^2)=26} \atop {b_1(1+q^2)=20}} \right. ~~~\Rightarrow~~~\\ \\ \\ \Rightarrow~~~ \left \{ {{20+b_1q=26} \atop {b_1+b_1q^2=20}} \right. ~~\Rightarrow~~~ \left \{ {{b_1q=6} \atop {b_1+6q=20}} \right. ~~\Rightarrow~~\\ \\ \\ \Rightarrow~~~ \left \{ {{b_1=18} \atop {q=1/3}} \right. ~~~~~or~~~~~~ \left \{ {{b_1=2} \atop {q=3}} \right.
ПОКАЗАТЬ ОТВЕТЫ
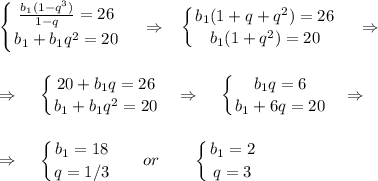
Другие вопросы по теме Алгебра
Neznayka133 Neznayka133  04.12.2021 20:57
Молю , бином ньютона .Нет разницы по какой формуле считать ?В интернете такой ответ ,а у меня другой и говорили решать по формуле которая на 2 фотке....
unicorncolever unicorncolever  04.12.2021 20:56
Алгебра 9 класс , правильно ли я решил данную задачу?...
kokorev861oxc4k3 kokorev861oxc4k3  04.12.2021 20:54
Решите уравнение и найдите все возможные корни: (x²+2x+2)(y²-4y+6)=2...
БлэтНэвэльный БлэтНэвэльный  04.12.2021 20:49
Определи значение выражения tgx, если tg(2п+х)=-3/11...
veronikasabrin veronikasabrin  04.12.2021 20:43
Даю тридцатку! С объяснением Нужно с 7 (правый столбец) по самый низ (до 3 в упростите выражение)...
oxle oxle  04.12.2021 20:41
Даю 20 б знайдіть найбільще і найменше значення функціі . Полное решение...
Luhfeeqq Luhfeeqq  12.09.2019 18:27
Запишите числовое выражение и найдите его значение произведение разности чисел 1 3/8 и 3 5/12 и числа 2,24 сумма числа 2,3 и частного чисел 1 2/9 и 3 1/6 ,...
Камилла200504 Камилла200504  12.09.2019 18:29
Степень с действительным показателем, как решить 3?...
andrewmikilov andrewmikilov  12.09.2019 18:29
Решить графическую систему уравнений {y=x-3 {y=-2x+3​...
froze1997 froze1997  12.03.2021 15:45
решить!Числовые не равенства!...

Популярные вопросы