Найдите первообразную для следующих функций, проходящую через точку а) f(x)=3x²-8x³+5, M(-2,10) б) f(x) = -8cosx, М( 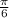,5)

Давайте начнем с первой задачи.

a) Для того чтобы найти первообразную функции f(x) = 3x²-8x³+5, нам нужно найти функцию F(x), производная которой равна f(x).

Шаг 1: Найдем первообразную для каждого члена функции f(x) по отдельности.

Для члена 3x², мы знаем, что производная функции x³ равна 3x². Таким образом, первообразная для этого члена будет x³.

Для члена -8x³, производная функции -2x⁴ равна -8x³. Следовательно, первообразная для этого члена будет -2x⁴.

Для члена 5, мы знаем, что производная константы равна нулю. Первообразная для этого члена будет 5x.

Шаг 2: Сложим найденные первообразные для каждого члена.

F(x) = x³ - 2x⁴ + 5x + C,

где C - произвольная постоянная.

Шаг 3: Найдем конкретное значение постоянной C, исходя из условия, что первообразная проходит через точку M(-2,10).

Подставим координаты точки M в уравнение первообразной:

10 = (-2)³ - 2(-2)⁴ + 5(-2) + C.

Простое вычисление покажет, что C = 27.

Итак, первообразная функции f(x) = 3x²-8x³+5, проходящая через точку M(-2,10), равна:

F(x) = x³ - 2x⁴ + 5x + 27.

Теперь перейдем ко второй задаче.

б) Для функции f(x) = -8cosx, чтобы найти первообразную, мы будем использовать известное правило, что первообразная синуса равна -cosx (с учетом постоянной).

То есть, F(x) = -8sinx + C.

Шаг 3: Найдем конкретное значение постоянной C, исходя из условия, что первообразная проходит через точку M( ,5).

Подставим координаты точки M в уравнение первообразной:

5 = -8sin() + C.

Простое вычисление покажет, что C = 13 + 4√3.

Итак, первообразная функции f(x) = -8cosx, проходящая через точку M(,5), равна:

F(x) = -8sinx + 13 + 4√3.

Это ответы на ваши вопросы. Если у вас остались еще вопросы, пожалуйста, не стесняйтесь задать их. Я готов помочь!