1. Алгебра
  2. Найдите p(x)+p(8-x), если

Найдите p(x)+p(8-x), если p(x)=\frac{x(8-x)}{x-4}, x\neq 4

TaHoC TaHoC    3   01.10.2019 12:10    12

Ответы
kartoshka212 kartoshka212  09.10.2020 07:45

Объяснение:

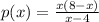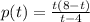Функцию   p(x)=\frac{x(8-x)}{x-4}  можно записать , обозначив переменную буквой t  (ведь от обозначения переменной функция не изменяется), получим  p(t)=\frac{t(8-t)}{t-4}  .

Это удобно сделать для того, чтобы потом вместо переменной  t  подставлять необходимое выражение  t=(8-x).

p(8-x)=\frac{(8-x)\cdot (8-(8-x))}{(8-x)-4}=\frac{(8-x)\cdot x}{4-x}=-\frac{x(8-x)}{x-4}\\\\\\p(x)+p(8-x)=\frac{x(8-x)}{x-4}-\frac{x(8-x)}{x-4}=0\; \; ,\; \; \; x\ne 4

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
UlianaUhanova UlianaUhanova  18.01.2021 16:44
Найдите наибольший отрицательный корень уравнения 8sinx+8cosx=sin2x+8...
DazaOtaku DazaOtaku  18.01.2021 16:45
Решите уравнение 5x2 − 15x = 0....
kadenets kadenets  18.01.2021 16:45
Розв яжіть графічно систему рівнянь {y²=x, y=x²​...
ХОРОШИСТ1234567891 ХОРОШИСТ1234567891  18.01.2021 16:46
Подайте у вигляді многочлена вираз:а) 3х³ (х² + 1), б) (с + 5)(с - 9), в) 5а²с(3а³с² – 2), г) c(x – 3) + d(x – 3).2. Спростіть вираз:а) -3у(у - 7) + 4,5у(6у - 2), б)...
mgurbo mgurbo  29.04.2020 14:50
найти значение выражения -x(x+7)+(x+5)(х-5) , при х=3/7...
ogxo ogxo  29.04.2020 14:50
Три вело туристи одночасно виїхали по одній дорозі з пункту А в пункт В. Їх середні швидкості становлять арифметичну прогресію, різниця якої дорівнює 3км/год. Велосипедисти...
lily20062601 lily20062601  29.04.2020 14:50
Решить уравнение заменой неизвестного (x-2)^4+(x-2)^2-2=0...
mrnaruto004ovx0o3 mrnaruto004ovx0o3  29.04.2020 14:50
Количество книг на первой полке втрое больше, чем на вто-рой. Если с первой полки снять 8 книг, а на вторую поставить2 книги, то на первой полке книг станет в 2 раза...
botejijofo botejijofo  29.04.2020 14:50
БІОЛОГІЯ що характерно для штучних екосистем а різний видовий складб саморегуляціяв однотипність видового складуг висока продуктивність​ багатьох видів...
vanyavanyaere vanyavanyaere  08.04.2021 17:38
решить Знайдіть значення добуткуa) (90 + 3) (90 - 3);6) 7,02 - 6,98B) 14,7. 13,3.​...

Популярные вопросы