Найдите одну из первообразных 1. f(x)=6x-9+3x⁵
2. f(x)=5cos(4x-2)+5x
3. f(x)=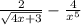
Другие вопросы по теме Алгебра
Популярные вопросы
- 4.Скільки 100°ої водяної пари треба направити на лід, температура...
3 - груз..ик, перевод..ик; плавиль..ик; обход..ик; копиров..ик; свар..ик....
2 - Подбери названия к разряд 2,3...
3 - Используя математический знак минус ...
1 - решать реакцию превращения CH4 = CH3 = CL = CH3 - CH3 = CO2 =NaHCO3...
3 - Напишите сообщение на тему У человека всегда есть выбор...
1 - Сколько протонов находится в ядре атома с атомным номером (атомным...
2 - 10xy-20y^= в^-aв= можно быстрее...
3 - что характерно из жизни станционных составителей рассказал автор...
3 - Бічні сторони трапеції 7см і 12см чому дорівнює P трапеції якщо...
1
Сначала найдем первообразную от каждой отдельной части функции:
∫6x dx = 3x²
∫-9 dx = -9x
∫3x⁵ dx = (3/6)x⁶ = (1/2)x⁶
Теперь сложим эти первообразные:
F(x) = 3x² - 9x + (1/2)x⁶
Таким образом, одной из первообразных функции f(x)=6x-9+3x⁵ является F(x) = 3x² - 9x + (1/2)x⁶.
2. Для нахождения первообразной функции f(x)=5cos(4x-2)+5x, мы должны найти функцию F(x), производная которой равна f(x).
Сначала рассмотрим первую часть функции: 5cos(4x-2).
Мы знаем, что ∫cos(x) dx = sin(x).
Также, мы знаем, что производная синуса sin(ax+b) равна cos(ax+b) * a.
Используя эти свойства, мы можем найти первообразную для cos(4x-2):
∫cos(4x-2) dx = (1/4) * ∫cos(4x-2) * 4 dx = (1/4) * sin(4x-2) = (1/4) * sin(4x-2).
Теперь рассмотрим вторую часть функции: 5x.
Производная для x² равна 2x.
Производная для (1/2)x² равна x.
Используя это, мы можем найти первообразную для 5x:
∫5x dx = (5/2) * ∫x dx = (5/2) * (1/2)x² = (5/4)x².
Теперь сложим эти первообразные:
F(x) = (1/4) * sin(4x-2) + (5/4)x².
Таким образом, одной из первообразных функции f(x)=5cos(4x-2)+5x является F(x) = (1/4) * sin(4x-2) + (5/4)x².
3. Для нахождения первообразной функции f(x) =2/√(4x+3) - 4/x⁵, мы должны найти функцию F(x), производная которой равна f(x).
Сначала рассмотрим первую часть функции: 2/√(4x+3).
Заметим, что производная для ln(x) равна 1/x. Также, производная для √x равна (1/2) * x^(-1/2).
Используя эти свойства, мы можем найти первообразную для 2/√(4x+3):
∫(2/√(4x+3)) dx = 2 * ∫(1/√(4x+3)) dx = 2 * ∫(1/(2√(x+(3/4)))) dx = 2 * ∫((1/2) * (x+(3/4))^(-1/2)) dx
= 4 * √(x + (3/4)).
Теперь рассмотрим вторую часть функции: -4/x⁵.
Производная для 1/x⁴ равна -4/x⁵. Также, мы можем заметить, что производная для ln(x) равна 1/x.
Используя эти свойства, мы можем найти первообразную для -4/x⁵:
∫(-4/x⁵) dx = ∫(-4 * x^(-5)) dx = -4 * ∫(x^(-5)) dx = -4 * (x^(-4)/(-4))
= x^(-4) = 1/(x^4).
Теперь сложим эти первообразные:
F(x) = 4 * √(x + (3/4)) + 1/(x^4).
Таким образом, одной из первообразных функции f(x) =2/√(4x+3) - 4/x⁵ является F(x) = 4 * √(x + (3/4)) + 1/(x^4).