Найдите один из корней уравнения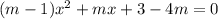
если другой равен (- 3)​

1,5

Объяснение:

Подставим x=-3 и найдем m

Подставим m=3 в исходное уравнение

Полученное квадратное уравнение решаем либо через дискриминант и находим второй корень

Либо по теореме Виета:

(m-1)x² + mx + (3-4m)=0

x1=-3

9(m-1)-3m+3-4m=0

9m-9-3m-4m+3=0

2m=6; m=3

(3-1)х²+3х+3-12=0

2х²+3х-9=0

D=9+4*2*9=9+72=81=9²

х2=(-3+9)/4=1,5

х1=(-3-9)/4=-12/4=-3

ответ: х2=1,5.