Найдите общее и частное решение дифференциального уравнения, удовлетворяющее начальным условием y=y0 при x=x0 ydx=(x+1)dy. y(0)=1
Другие вопросы по теме Алгебра
Популярные вопросы
- Допишите уравнение реакции и определите сумму коэффициентов: f2+h2o...
3 - Вычеслите используя закон сложения б)19/55+18/55+12/55,д)...
2 - Указать причины марафонской битвы.! 5 класс...
3 - Решить ! 3/7(-0,54)-1,56*3/7 -0,77*4/9-4/9*2,83...
1 - Найдите значениевыражение5,02•3,8+5,02•6,2...
1 - Черепаха тортила 5ч ползла со скоростью 4км/ч всего ей надо проползти 48км...
2 - Как составить приглашение на детский праздник используя слова афиша карусель...
2 - Реши уравнения 45-32: у=37 63: (24 - х : 3)=7...
3 - Длина прямоугольника на 75 % больше его ширины. периметр прямоугольника составляет...
3 - Объясни какие свойство сложение и вычитания отражения в данных выражениях...
3
Используем условие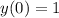 :
: