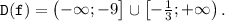Найдите область определения выражения f(x): корень 3x²+28x+9 если
Другие вопросы по теме Алгебра
Популярные вопросы
- Позначте рядок, у якому записано лише сполучники: А) бо, а, та, начебто, багато;...
2 - составить 10 во с ответами S 60. Физико-географическиестраны ЕвразииБольшие...
3 - РАЗБЕРИТЕ СЛОВОСОЧЕТАНИЯ ИХ 6 ВОТ ПРИМЕР (ХОЛОДНЫЙ ДОЖДЬ) ДОЖДЬ (КАКОЙ ?)ХОЛОДНЫЙ...
1 - Буду благодарна. АВ – хорда кола з центром у точці О. У цьому колі проведено...
3 - разгадайте кроссворд по фото...
1 - Найдите периметр прямоугольника если одна из сторон равна 1,9 а площадь 9,88...
1 - Составь и запиши текст о городе будущего. Используй понравишься опорные слова,...
2 - Можно ли назвать данный набор предложений текстом? Красоту,что дарит нам природа....
1 - Расскажите, с какого знаменательного события начинается рассказ В. П. Астафьева...
2 - Отметь, какое из утверждений верно для реакции соединения: 1) в реакцию вступают...
2
Т.к. подкоренное выражение должно быть неотрицательным, то необходимо следующее: 3x²+28x+9≥0.
Решим неравенство графически. Найдём нули функции y=3x²+28x+9.
Графиком функции y=3x²+28x+9, будет парабола, ветви которой направлены вверх т.к. 3>0.
Графическое решение смотри в приложении.
Запишем решение множеством: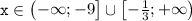
ответ: