Найдите область определения функции
а)у=4х-15 /(дробь) 7-8х+Х²
б)у=√11-х²

Ответы

vovabondar28 15.01.2021 21:12

а)

$y = \dfrac{4x-15}{7+8x+x^2}$

Знаменатель дроби не должен быть равен нулю. Получаем:

$7+8x+x^2 \neq 0\\\\x^2 + 8x + 7 \neq 0$

Чтобы это решить, для начала представим, что это выражение равно нулю, тогда получим квадратное уравнение и найдём его корни.

$x^2 + 8x + 7 = 0\\\\D = b^2 - 4ac = 8^2 - 4\cdot 1\cdot 7 = 64 - 28 = 36\\\\x_{1} = \dfrac{-b+\sqrt{D}}{2a} = \dfrac{-8 + 6}{2} = \dfrac{-2}{2} = \boxed{-1}\\\\\\x_{2} = \dfrac{-b-\sqrt{D}}{2a} = \dfrac{-8 - 6}{2} = \dfrac{-14}{2} = \boxed{-7}$

Но так как изначально это выражение было неравно нулю, то из области определения просто вычёркиваются корни уравнения, решённого нами выше.

ответ: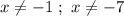 $x \neq -1\ ;\ x \neq -7$ .

б)

$y = \sqrt{11-x^2}$

Подкоренное выражение всегда неотрицательно, то есть, больше или равно нулю.

$11-x^2 \geq 0\\\\(\sqrt{11} - x)(\sqrt{11} + x) \geq 0$

Решим неравенство методом интервалов.

Нули: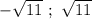 $-\sqrt{11}\ ;\ \sqrt{11}$

- + -

--------------------- $\bullet$ --------------------------

$-\sqrt{11}$ $\sqrt{11}$

Нам нужно найти те промежутки, где выражение больше или равно нулю. Такой промежуток только один: $[-\sqrt{11}\ ;\ \sqrt{11}]$ , так как там "+". Этот промежуток и будет являться областью определения функции.